אי-שוויון ברנולי

המחשה גרפית של אי-שוויון ברנולי, עבור n=3

באנליזה מתמטית, אי-שוויון ברנולי הוא אי-שוויון יסודי ושימושי, המאפשר להעריך את הביטוי ${\displaystyle \ (1+x)^{n}}$. האי-שוויון קובע ש- ${\displaystyle \ (1+x)^{n}\geq 1+nx}$ לכל מספר שלם ${\displaystyle \ n\geq 0}$ ולכל מספר ממשי ${\displaystyle \ x>-1}$. את האי-שוויון אפשר להוכיח באינדוקציה.

בעזרת אי-שוויון זה אפשר להראות שהסדרה ${\displaystyle \ \left(1+{\frac {1}{n}}\right)^{n}}$ עולה בזמן שהסדרה ${\displaystyle \ \left(1+{\frac {1}{n}}\right)^{n+1}}$ יורדת, וכך להגדיר את בסיס הלוגריתם הטבעי, ${\displaystyle \ e=2.718...}$, כגבולן המשותף.

תחולה

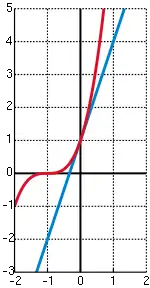
אי השוויון נכון לכל ${\displaystyle \,n}$ ממשי, ובלבד ש-${\displaystyle \ n\geq 1}$ (את ההכללה אפשר להוכיח על ידי השוואת הנגזרות של שני האגפים). כאשר n טבעי זוגי, אי השוויון נכון לכל ${\displaystyle \ x}$, וכאשר n אי-זוגי, הוא נכון לכל ${\displaystyle \ -2<x}$ (ואף מעט משמאל לנקודה 2-).

הוכחה באינדוקציה לאי-שוויון ברנולי

בסיס האינדוקציה: ${\displaystyle \ n=1}$ ואכן מתקיים ש: ${\displaystyle \ (1+x)^{1}\geq 1+1\cdot x}$ כלומר: ${\displaystyle \ 1+x\geq 1+x}$ .

הנחת האינדוקציה: נניח את נכונות הטענה עבור ${\displaystyle \ n=t}$ כלשהו, כלומר נניח ש: ${\displaystyle \ (1+x)^{t}\geq 1+tx}$, נשים לב לכך שמכיוון ש-${\displaystyle \ x>-1}$ אז: ${\displaystyle \ (x+1)>0}$, ולכן ניתן לכפול את שני אגפי האי-שוויון של ההנחה ולקבל ש: ${\displaystyle \ (1+x)\cdot (1+x)^{t}\geq (1+x)\cdot (1+tx)}$ כלומר: ${\displaystyle \ (1+x)^{t+1}\geq 1+tx+x+tx^{2}}$

צעד האינדוקציה: צריך להוכיח את נכונות הטענה עבור ${\displaystyle \ n=t+1}$ כלומר צריך להוכיח ש-${\displaystyle \ (1+x)^{t+1}\geq 1+(t+1)\cdot x}$, כלומר: ${\displaystyle \ (1+x)^{t+1}\geq 1+tx+x}$, אבל מתוך הנחת האינדוקציה הראינו כי: ${\displaystyle \ (1+x)^{t+1}\geq 1+tx+x+tx^{2}}$, הביטוי ${\displaystyle \ tx^{2}}$ חיובי (כי ${\displaystyle \ x^{2}\geq 0}$ וגם ${\displaystyle t\geq 0}$) ולכן ממילא מתקיים ש-${\displaystyle \ (1+x)^{t+1}\geq 1+tx+x+tx^{2}\geq 1+tx+x}$.

הכללה

לכל חזקה ממשית ${\displaystyle r\,}$ ניתן להכליל את האי-שוויון כך שעבור כל ${\displaystyle r\notin (0,1)}$ ולכל ${\displaystyle \ x>-1}$

${\displaystyle (1+x)^{r}\geq 1+rx}$

ועבור כל ${\displaystyle r\in [0,1]}$

${\displaystyle (1+x)^{r}\leq 1+rx}$

כאמור, את ההכללה אפשר להוכיח בעזרת הנגזרת.