גרעין (תורת הקטגוריות)

בתורת הקטגוריות, גרעין הוא מושג כללי המכליל את מושג הגרעין האלגבראי - דהיינו גרעין של הומומורפיזם של חבורות, חוגים ומודולים.

באופן לא לגמרי פורמלי, גרעין של מורפיזם ${\displaystyle \,f:X\rightarrow Y}$ עבור ${\displaystyle X,Y}$ אובייקטים כלשהם, הוא האובייקט ${\displaystyle K}$ "הכללי ביותר" עם מורפיזם מתאים מהצורה ${\displaystyle \,k:K\rightarrow X}$, כך ש-${\displaystyle \,f\circ k=0}$.

הגדרה

תהי ${\displaystyle C}$ קטגוריה, המכילה את מורפיזם האפס. יהיו ${\displaystyle X,Y}$ אובייקטים ויהי ${\displaystyle \,f:X\rightarrow Y}$ מורפיזם.

הגרעין של ${\displaystyle f}$ הוא אובייקט ${\displaystyle \ker(f)}$ שעבורו קיים מורפיזם ${\displaystyle k:\ker(f)\to Y}$ שהוא המשווה של ${\displaystyle f}$ ושל מורפיזם האפס ${\displaystyle 0_{X,Y}:X\to Y}$, וכן ${\displaystyle \ker(f)}$ אוניברסלי ביחס לתכונה זו של קיום ${\displaystyle k}$.

באופן מפורש, גרעין הוא אובייקט המקיים את שתי התכונות הבאות:

• ${\displaystyle \,f\circ k=0_{K,Y}}$, כלומר הדיאגרמה הבאה קומוטטיבית:

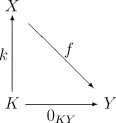
• בהינתן אובייקט ${\displaystyle K'}$ עם מורפיזם כלשהו ${\displaystyle \,k':K'\rightarrow X}$ כך ש-${\displaystyle \,f\circ k'=0_{K',Y}}$, קיים מורפיזם יחיד ${\displaystyle \,u:K'\rightarrow K}$ כך ש ${\displaystyle \,k\circ u=k'}$. כלומר הדיאגרמה הבאה קומוטטיבית:

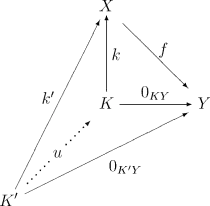
במקרים רבים, במיוחד באלגברה, מתייחסים לגרעין כאל הגרעין האלגברי, וההמורפיזם ${\displaystyle k}$ הוא העתקת ההכלה הטבעית.

ניתן להראות כי k הוא תמיד מונומורפיזם.

לא לכל מורפיזם בהכרח קיים גרעין, אך אם קיים גרעין אז הוא יחיד עד כדי איזומורפיזם.

דוגמאות

• בקטגוריה של חבורות, בהינתן הומומורפיזם ${\displaystyle \,f:X\rightarrow Y}$, אם K הוא הגרעין של f במובן הרגיל של המילה, אז K היא תת-קבוצה של X, ומורפיזם ההכלה ${\displaystyle \,k:K\rightarrow X}$ הוא הגרעין של f במובן הקטגורי.
• בקטגוריה של חוגים אין גרעין, משום שאין בקטגוריה זו מורפיזם אפס. (שהרי מניחים כי הומומורפיזמים מעתיקים את היחידה ליחידה).