טרקטריקס

טרקטריקס (אנגלית: Tractrix) הוא עקומה לאורכה נע עצם כאשר הוא נמשך על גבי מישור אופקי על ידי קטע ישר המחובר בקצהו השני לנקודה הנעה (מושכת) לאורך קו ישר המאונך לקו ההתחלתי המחבר בין הנקודה המושכת והעצם. זהו על כן סוג של עקום מרדף.

הוא הוצג לראשונה על ידי Claude Perrault ב-1670, ונחקר מאוחר יותר על ידי אייזק ניוטון ב-1676 וכריסטיאן הויגנס ב-1692.

שם העקומה נגזר מהפועל הלטיני "trahere", שפירושו למשוך או לגרור.

גזירה מתמטית

יצירת טרקטריקס באמצעות גרירת עצם

נניח כי העצם ממוקם ב-עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (a,0)} והנקודה המושכת היא בראשית, כך ש-${\displaystyle a}$ הוא אורך המוט המושך. הנקודה המושכת מתחילה לנוע לאורך הכיוון החיובי בציר עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle y} .

בכל רגע, המוט יהיה משיק לעקום עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle y=y(x)} שמתאר העצם, כך שמסלולו הופך תלוי לגמרי בתנועה של הנקודה המושכת.

כיוון שגם אורך המוט קבוע בערכו ושווה ל-${\displaystyle a}$ , אז מקבלים מתמטית כי מסלול העצם מקיים את המשוואה הדיפרנציאלית:

${\displaystyle {\frac {dy}{dx}}=-{\frac {\sqrt {a^{2}-x^{2}}}{x}}}$

יחד עם תנאי ההתחלה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle y(a)=0} . פתרון המשוואה הדיפרנציאלית הוא:

עיבוד הנוסחה נכשל (שגיאת המרה. השרת ("https://en.wikipedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle {\begin{aligned}y=\int \limits _{x}^{a}{\frac {\sqrt {a^{2}-t^{2}}}{t}}\,dt=\pm {\Bigg (}a\ln \left({\frac {a+{\sqrt {a^{2}-x^{2}}}}{x}}\right)-{\sqrt {a^{2}-x^{2}}}{\Bigg )}\end{aligned}}}

כאשר האבר הראשון בפתרון הזה ניתן לכתיבה גם: ${\displaystyle a\,{\text{arsech}}\left({\frac {x}{a}}\right)}$ .

הענף השלילי של הפתרון מייצג את המקרה שבו הנקודה המושכת נעה בכיוון השלילי של ציר עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle y} . שני הענפים שייכים לטרקטריקס, ונפגשים בנקודת החוד (cusp) שהקואורדינטות שלה הן עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (a,0)} .

חשיבות העקום

משמעות חשובה לעקומה נגזרת מחקר גוף הסיבוב שלו מסביב לאסימפטוטה שלו; הפסאודו-ספירה. משטח הפסאודו-ספירה, שנחקר בידי אוגניו בלטרמי ב-1868 כמשטח בעל עקמומיות גאוס שלילית קבועה, הוא מודל מקומי של גאומטריה לא-אוקלידית (במקרה זה של גאומטריה היפרבולית).

תכונות

קו השרשרת כאבולוט של הטרקטריקס

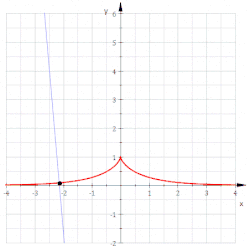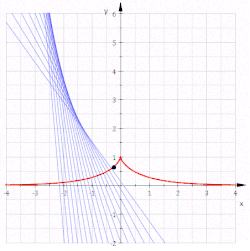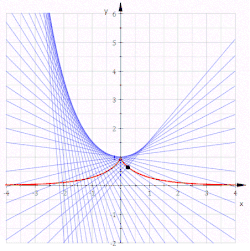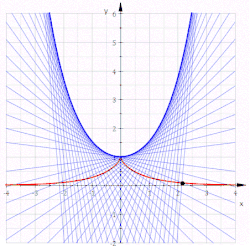
• התכונה הבסיסית של הטרקטריקס, שנגזרת ישירות מהדרך הגאומטרית בה הוא מוגדר, היא שלכל נקודה עליו, למקטע של הקו המשיק לו שמחבר בין נקודת ההשקה ונקודת החיתוך שלו עם האסימפטוטה, יש אורך קבוע ${\displaystyle a}$ .
• אורך העקום בין נקודות ${\displaystyle x=x_{1},x_{2}}$ הוא עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a\ln\left(\frac{x_1}{x_2}\right)} .
• השטח בין הטרקטריקס לאסימפטוטה שלו הוא עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \frac{\pi}{2}a^2} .
• המעטפת של קווי הנורמל של הטרקטריקס (שהיא גם האוולוט שלו) היא קו השרשרת שמשוואתו נתונה על ידי עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle y=a\cosh\left(\frac{x}{a}\right)} .

המחשה יפהפיה לעובדה זאת היא דרך הסתכלות בתלת-ממד על גופי הסיבוב של הטרקטריקס ושל האוולוט שלו. בניית הקווים הנורמלים למשטח בעלת עקמומיות גאוס שלילית קבועה (שהוא כפי שצוין מקודם, גוף סיבוב של הטרקטריקס) מייצרת מעטפת שהיא בהכרח משטח מינימלי (minimal surface); משטח שממזער את שטח הפנים שלו בהינתן תנאי שפה נתונים.

הוכחה לטענה זאת היא דרך הכללת המשפטים המתארים אוולוטים של עקומות במישור לכדי אוולוטים של משטחים במרחב; במקרה של משטח מרחב, אלמנט השטח של משטח האוולוט ${\displaystyle dA}$ הוא עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle dR_1dR_2} כאשר עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle R_1,R_2} הם רדיוסי העקמומיות הראשיים שלה המשטח המקורי בנקודה. עובדה זאת היא הגירסה המרחבית למשפט הקובע שאורך האוולוט של עקום שווה להפרש בין רדיוסי העקמומיות שלו בנקודות הקצה שלו. מהכללה זאת ומהעובדה שהמכפלה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle R_1R_2} קבועה על הפסאודו-ספירה, מקבלים ששטח האוולוט שלה הוא בהכרח אקסטרמלי. לפיכך האוולוט של גוף הסיבוב של הטרקטריקס הוא בהכרח קטנואיד; המשטח המינימלי היחיד בעל סימטריה גלילית, ומכאן שבחתך מישורי האוולוט של הטרקטריקס הוא קו השרשרת.

מכונות שרטוט

• ב-1693, תיאר לייבניץ תיאר מכניזם שיכול לבצע תרבוע מכני של עקומים. המכניזם, דוגמא מוקדמת למנגנון של "אינטגרף" (integraph), היה מבוסס על תכונות עקומת הטרקטריקס.
• ב-1706 בנה ג'ון פרקס מכונה המבוססת על תכונות העקום שיכלה לבצע תרבוע היפרבולי.
• ב-1729 בנה יוהאן פולני מכונה דומה המאפשרת לשרטט עקומים לוגריתמיים.

ראו גם

• פסאודו-ספירה