משפט הזווית החיצונית במשולש

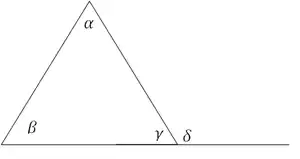
הזווית החיצונית δ∢ שווה לסכום α+∢β∢

בגאומטריה אוקלידית, משפט הזווית החיצונית קובע כי זווית חיצונית במשולש שווה בגודלה לסכום שתי הזוויות הפנימיות שאינן סמוכות לה. זהו ניסוח מחדש של העובדה שסכום הזוויות במשולש שווה לזווית שטוחה: בשרטוט, α+∢β+∢γ=180°=∢γ+∢δ∢, ולכן α+∢β=∢δ∢.

ממילא נובע שזווית חיצונית גדולה מכל זווית פנימית של המשולש שאינה סמוכה לה.

הוכחת המשפט

נתבונן במשולש ABC. נראה שהזווית C שווה לסכום הזוויות האחרות. תהי Y נקודה על המשך הקטע AC. העבר מ-C ישר CX המקביל ל-AB. הזווית החיצונית ל-C, שהיא הזווית BCY, שווה לסכום הזוויות XCY ו-BCX. אולם XCY=BAC בהיותן זוויות מקבילות, ו-BCX=ABC בהיותן זוויות משלימות. לכן BCY=BCX+XCY=ABC+BAC=a+b.

לקריאה נוספת

בני גורן, גאומטריה של המישור
"אפשר גם אחרת" כיתה ט - חלק א', תשע"ו

הערך באדיבות ויקיפדיה העברית, קרדיט,
רישיון cc-by-sa 3.0

This article is issued from Hamichlol. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.