עקמומיות

גרפים אליפטיים המתאפיינים בעקמומיות שונה

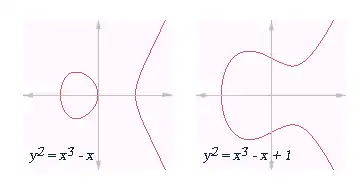
באופן כללי, עקמומיות היא מידת הכפיפה וההתעקמות של דבר מה. המונח עשוי להתייחס לישויות גאומטריות שונות, החל מקווים ועד למרחבים מממדים גבוהים, ולכן העקמומיות, מידת הסטייה מן המצב המוגדר כישר או שטוח, מוגדרת ומחושבת בצורות ושיטות שונות. עקמומיות עשויה להוות סקלר (גודל כמותי חסר כיוון) או וקטור – גודל המתאפיין בכיוון.

עקמומיות עקומה

עקמומיות עקומה מוגדרת כגבול היחס בין הפרש זוויות השיפוע (המשיקים) בשתי נקודות סמוכות על העקומה, לבין אורך המסילה המחברת שתי נקודות אלו, כאשר זה שואף לאפס:

${\displaystyle k=\lim _{\Delta s\to 0}{\frac {\Delta \theta }{\Delta s}}={\frac {d\theta }{ds}}}$

כאשר עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Delta\theta} הפרש הזוויות ו-${\displaystyle \Delta s}$ אורך המסילה.

עקמומיות הקו בנקודה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle P} שווה לערך ההפוך של רדיוס העקמומיות ${\displaystyle r}$ בנקודה

אם משוואת העקומה היא עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle y=f(x)} כי אז מתקיים עבור זווית שיפוע המשיק לעקומה בנקודה כי עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle y'(x)=\tan(\theta)} , ולכן העקמומיות היא:

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle k=\frac{d\theta}{ds}=\frac{y''}{\sqrt{(1+y'^2)^3}}}

גודל זה שווה לערך ההפוך של רדיוס העקמומיות בנקודה (רדיוס המעגל הנושק – המעגל המתלכד עם העקומה בנקודה). כלומר,

${\displaystyle k={\frac {1}{R}}}$

ומכאן שרדיוס העקמומיות קטן ככל שהעקמומיות גדלה.

במקרה של קו ישר, העקמומיות שווה לאפס, שכן הנגזרת השנייה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle y} מתאפסת. רדיוס העקמומיות במקרה זה הוא אינסופי.

עקמומיות משטח

עקמומיות של מרחב

עקמומיות שלילית וחיובית

נקודת אוכף על גרף הפונקציה ${\displaystyle z=x^{2}-y^{2}}$ (אדום). פני המשטח מתעקלים מעלה מן הנקודה בעקמומיות חיובית ומטה ממנה בעקמומיות שלילית

ניתן להבחין בין כיוון ההתעקלות של עקומות באמצעות סימונם. כאשר, עקמומיות חיובית (עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle k>0} ) מציינת התעקלות כלפי מעלה (רדיוס העקמומיות בנקודה מכון כלפי מעלה), ועקמומיות שלילית (${\displaystyle k<0}$) מציינת התעקלות כלפי מטה (רדיוס העקמומיות בנקודה מכון כלפי מטה). כיוון העקמומיות הוא תלוי נקודת מבט, והיפוכה ישנה את מראית כיוון ההתעקלות וכפועל יוצא, סימן העקמומיות.

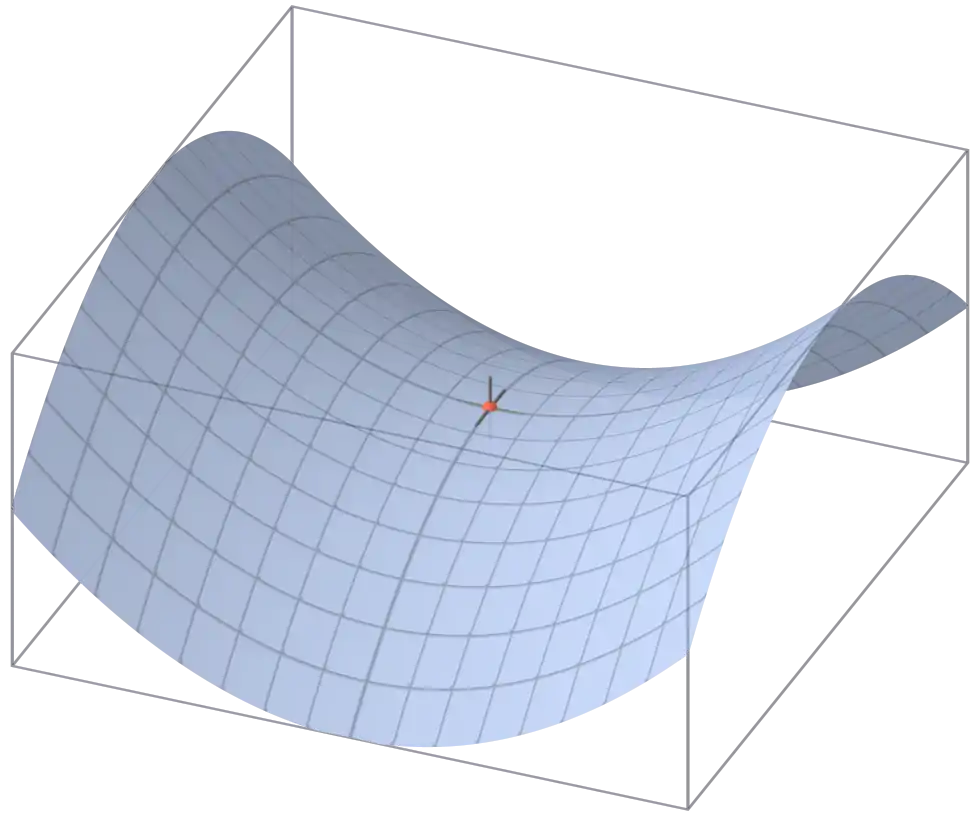
בהתייחס למשטחים עקומים, ייתכנו מקרים, כזה של מבנה בעל צורת אוכף, בהם אחת העקמומיות הראשיות בנקודה היא חיובית ואילו השנייה היא שלילית. עקמומיות גאוס (עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle Q} ) עבור נקודה שכזו תהא שלילית ואילו רדיוס העקמומיות יהיה מספר מדומה (השורש הריבועי של הערך ההפוך של עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle Q} ).

עקמומיות חיצונית ופנימית

עקמומיות היא תכונה של המרחב, יהא ממדו אשר יהא, הגלויה לעיני צופה חיצוני, אך יש שניתן לזהותה גם מתוך המרחב עצמו, באמצעות חקירת התכונות של עצמים גאומטריים במרחב. עקמומיות פנימית היא עקמומיות מן הסוג השני, תכונה שגם 'תושבי' המרחב יכולים לזהותה ולא רק צופים חיצוניים. לעומת זאת, עקמומיות חיצונית היא עקמומיות שלא ניתן להבחין בה מתוך המרחב עצמו והיא מובחנת רק לעיני צופה חיצוני, ממד גבוה יותר. עקמומיות קו, למשל, היא עקמומיות חיצונית. תושבי הקו לא יבחינו בעקמומיותו, אף לא באמצעות חישובים ומדידות.

עקמומיות גאוס, עקמומיות משטח, היא דוגמה לעקמומיות פנימית ולפי התאורמה אגרגיום (משפט בגאומטריה דיפרנציאלית שהוכח על־ידי קרל פרידריך גאוס) ניתן לזהותה באמצעות חקירת התכונות של עצמים גאומטריים במרחב. היחס בין הקף מעגל לקוטרו, וסכום הזוויות במשולש, הן שתיים מן התכונות הגאומטריות שבאמצעותן ניתן לזהות עקמומיות פנימית ולחשבה. תכונות אלו משתנות כתלות בעקמומיות הפנימית של המרחב: במישור (משטח שטוח) בו העקמומיות היא 0, שטח מעגל הוא עיבוד הנוסחה נכשל (שגיאת המרה. השרת ("https://en.wikipedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle \pi R^{2}} וסכום הזוויות במשולש הוא עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \pi} ; עבור משטח המתאפיין בעקמומיות פנימית נקבל תוצאות שונות, המעידות על סטייתו מהמצב השטוח, ובאמצעותן נוכל להעריך את עקמומיותו. ביצוע מדידות מעין אלו בנקודות שונות של המשטח תאפשר שרטוט של מפת עקמומיותו.

עקמומיות אמיתית ועקמומיות מדומה

עקמומיות מדומה, להבדיל מעקמומיות אמיתית, היא עקמומיות שניתן לסלקה, באמצעות טרנספורמציה מתאימה, מבלי לשנות את תכונות המרחב. משטח גלילי ומשטח חרוטי הם דוגמאות למשטחים בעלי עקמומיות מדומה, שניתן לפרשם למישור מבלי לשנות את תכונותיהם. משטח כדורי לעומת זאת הוא משטח בעל עקמומיות אמיתית ופרישתו תייצר מתיחות וחיתוכים.

עקמומיותו של משטח היא מדומה אם בכל נקודה על פניו ניתן למצוא לפחות כיוון אחד שבו קיים קו ישר הכלול במשטח עצמו. קווים מעין אלו מציינים למעשה את קיומו של כיוון או מספר כיוונים שבהם העקמומיות במשטח היא אפס, ומעידים על האפשרות לסלק את העקמומיות באמצעות טרנספורמציה למערכת ייצוג שטוחה. אם בכל נקודה על פני משטח בעל עקמומיות מדומה, נבנה מערכת מקומית שטוחה (מישור מקומי המשיק למשטח בנקודה), ניתן יהיה לחבר את כלל המערכות השטוחות שניבנו לאורך קו שכזה לכדי מערכת שטוחה אחת, נעדרת עקמומיות.

בהתייחס למרחבים מממדים שונים, מרחב שרכיבי הטנזור שלו קבועים הוא מרחב שטוח או בעל עקמומיות מדומה. ומרחב שחלק או כל רכיבי הטנזור שלו הם משתנים תלויים הוא מרחב בעל עקמומיות אמיתית.