פונקציה קוונטית

פונקציה קוונטית הוא מעגל שערים קוונטיים אשר מממש חישוב של פונקציה כלשהי $\left.f(x):\{0,1\}^{n}\to \{0,1\}\right.$ .

בניית מעגל הפיך מפונקציה כלשהי

נרצה כי המעגל קוונטי יוכל לחשב פונקציה כלשהי ללא הגבלה על תכונותיה, ובפרט פונקציה שאינה נדרשת להיות הפיכה או חד-חד ערכית. מאידך, חוקי המכניקה הקוונטית, מאלצים כל מעגל חישוב קוונטי להיות הפיך. כדי להתגבר על אילוץ זה ועדיין לאפשר חישוב של כל פונקציה, המעגל מממש בפועל חישוב של פונקציה הפיכה, שנסמנה עיבוד הנוסחה נכשל (שגיאת המרה. השרת ("https://en.wikipedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle F(x):\{0,1\}^{n+1}\to \{0,1\}^{n+1}} אשר בעזרתה ניתן לחשב את הפונקציה המקורית $\left.f(x)\right.$ .

מעגל הפונקציה החדשה F מקבל, בנוסף ל-n הקיוביטים המייצגים את עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \left.x\right.} , קיוביט נוסף אשר נקרא קיוביט המטרה (target). מוצא המעגל אינו משנה את n הקיוביטים אשר מייצגים את עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \left.x\right.} (כך מתקבלת ההפיכות), אך קיוביט המטרה משתנה לערך $f(x)\oplus b$ , כאשר b הוא הערך של קיוביט המטרה בכניסת המעגל. בפרט, אם קיוביט המטרה מאותחל לערך ההתחלתי עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle |0\rangle} , במוצא המעגל ייתקבל קיוביט במצב קוונטי $|f(x)\rangle$ .

מעגל קוונטי הפיך לחישוב הפונקציה הכללית

\left.f(x)\right.

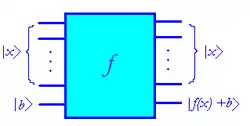
בניסוח מתמטי, עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle |x\rangle|b\rangle\stackrel{F}{\to}|x\rangle|f(x)\oplus b\rangle} כאשר $|x\rangle$ מצב קוונטי בבסיס החישוב של n קיוביטים, ו- $|b\rangle$ הוא מצב קוונטי של קיוביט בודד בבסיס החישוב.

הרחבה למצב קוונטי כלשהו

לפי עיקרון הליניאריות, ניתן להרחיב את החישוב לכל מצב קוונטי $|x\rangle$ על ידי פירוק המצב לסופרפוזיציה של מצבי בסיס החישוב, וביצוע החישוב על כל אחד מהם בנפרד. נניח שבכניסת המעגל מאותחל האוגר למצב עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle |x\rangle=|+\rangle} , כאשר קיוביט המטרה כבוי $b=0$ .

נפרק את אוגר הכניסה לסופרפוזיציה של אברי בסיס החישוב: עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle |x\rangle=\frac{1}{\sqrt{2}}\left(|0\rangle+|1\rangle\right)}
נבצע את החישוב על כל חלק בנפרד:

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle |x\rangle|b\rangle = \frac{1}{\sqrt{2}}\left(|0\rangle+|1\rangle\right)|0\rangle = \frac{1}{\sqrt{2}}\left(|0\rangle|0\rangle+|1\rangle|0\rangle\right) \stackrel{F}{\to} \frac{1}{\sqrt{2}}\left(|0\rangle|f(0)\rangle+|1\rangle|f(1)\rangle\right)}

שימושים

בניית מעגל הפיך למימוש פונקציה שרירותית היא הבסיס לחישוב קוונטי, ונעשה בה שימושים רבים עבור אלגוריתמים המקבלים פונקציה בתור הקלט של האלגוריתם, כפי שמבוצע באלגוריתם דויטש-ג'וזה ואלגוריתם סימון. שימוש זה מקביל להפעלת אורקל בחישוב קלאסי.

הערך באדיבות ויקיפדיה העברית, קרדיט,
רישיון cc-by-sa 3.0

This article is issued from Hamichlol. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.