פונקציית פוליגמא

גרף של פונקציית גמא מסדר 0, 1, 2 ו-3

במתמטיקה, פונקציית הפוליגמא מסדר m היא פונקציה מרומורפית אשר מוגדרת על ידי הנגזרת של הלוגריתם של פונקציית גמא:

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \psi^{(m)}(z) := \frac{d^m}{dz^m} \psi(z) = \frac{d^{m+1}}{dz^{m+1}} \ln\Gamma(z).}

אז

${\displaystyle \psi ^{(0)}(z)=\psi (z)={\frac {\Gamma '(z)}{\Gamma (z)}}}$

כאשר Γ(z) היא פונקציית גמא. פונקציית הפוליגמא היא פונקציה הולומורפית בתחום עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \C \setminus -\N_0} .

גרף במישור המרוכב של פונקציית הפוליגמא

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ln\Gamma(z) }	עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \psi^{(0)}(z) }	עיבוד הנוסחה נכשל (שגיאת המרה. השרת ("https://en.wikipedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle \psi ^{(1)}(z)}
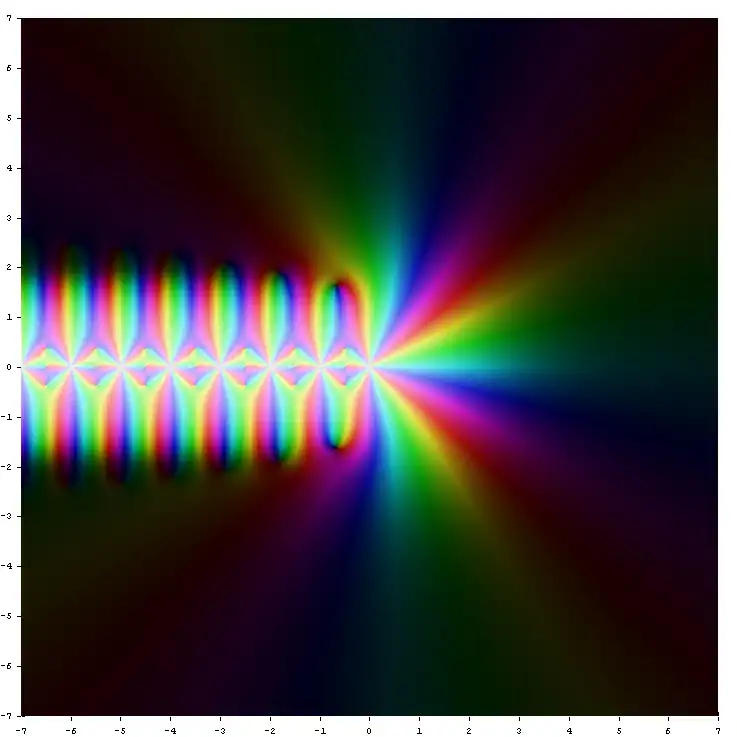${\displaystyle \psi ^{(2)}(z)}$	עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \psi^{(3)}(z) }	עיבוד הנוסחה נכשל (שגיאת המרה. השרת ("https://en.wikipedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle \psi ^{(4)}(z)}

נוסחה על ידי אינטגרל

אפשר להגדיר את פונקציית פוליגמא על ידי אינטגרל:

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \psi^{(m)}(z)= (-1)^{m+1}\int_0^\infty\frac{t^m e^{-zt}} {1-e^{-t}}\ dt =-\int_0^1\frac{t^{z-1}}{1-t}\ln^mt\ dt }

נוסחת נסיגה

וגם על ידי נוסחת נסיגה

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \psi^{(m)}(z+1)= \psi^{(m)}(z) + \frac{(-1)^m\,m!}{z^{m+1}}}

או על ידי

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \frac{\psi^{(m)}(n)}{(-1)^{m+1}\,m!} = \zeta(1+m) - \sum_{k=1}^{n-1} \frac{1}{k^{m+1}} = \sum_{k=n}^\infty \frac{1}{k^{m+1}} \qquad m \ge 1}

כאשר

${\displaystyle \psi ^{(0)}(n)=-\gamma \ +\sum _{k=1}^{n-1}{\frac {1}{k}}}$

לכול n טבעי.

טור טיילור

טור טיילור של פונקציית הפוליגמא היא:

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \psi^{(m)}(z+1)= \sum_{k=0}^\infty (-1)^{m+k+1} \frac {(m+k)!}{k!} \; \zeta (m+k+1)\; z^k \qquad m \ge 1}

כאשר

${\displaystyle \psi ^{(0)}(z+1)=-\gamma +\sum _{k=1}^{\infty }(-1)^{k+1}\zeta (k+1)\;z^{k}}$

אשר מתכנס כאשר לכל z בעל ערך מוחלט של 1. במקרה זה זטא מוגדרת להיות פונקציית זטא של רימן.

שימושים

קישורים חיצוניים

• פונקציית פוליגמא באתר Wolfram MathWorld