קינטיקת מיכאליס-מנטן

קינטיקת מיכאליס-מנטן מתארת את הקינטיקה של אנזימים רבים. היא קרויה על שמם של לאונור מיכאליס ומוד מנטן. מודל קינטי זה תקף רק כאשר ריכוז האנזים קטן בהרבה מריכוזו של המצע (הסובסטרט) ורק כאשר האנזים הוא לא אלוסטרי. בעזרת המשוואה ניתן לדעת את מהירות התגובה של אנזים מסוים בריכוז מסוים וזאת ע"פ המשוואה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle V= \frac{V_{max}[S]}{K_m + [S]}}

הגדרת הקבועים

דיאגרמת מהירות תגובה וקבוע מיכאליס-מנטן (K_m)

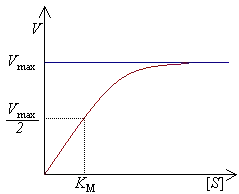
כדי לקבוע את הקצב המרבי של תגובה בתיווך אנזים, ריכוז הסובסטרט (מסומן כ-[S]) מוגדל עד שמושג קצב קבוע של היווצרות תוצר. זוהי המהירות המרבית (המסומנת ב-V_max) של האנזים. במצב זה האתר הפעיל (או האתרים הפעילים) של האנזים רווים בסובסטרט. במהירות המרבית, הפקטורים הנוספים אשר משפיעים על קצב התגובה (כגון pH וטמפרטורה) מצויים בערכים אופטימליים.

מהירות התגובה

המהירות (מסומנת כ-V) פירושה מספר התגובות לשנייה, אשר מזורזות על ידי האנזים. עם הגדלת ריכוז הסובסטרט, האנזים מתקרב באופן אסימפטוטי למהירותו המרבית V_max, אך למעשה לא יכול להגיע אליה. כיוון שכך לא קיים [S] שמתאים ל-V_max. במקום זאת, הערך אשר מאפיין את האנזים מוגדר בריכוז הסובסטרט בחצי מהמהירות המרבית (V_max/2). ערך זה מסומן כ-K_m והוא נקרא גם קבוע מיכאליס-מנטן.

קבוע מיכאליס-מנטן

משום שלא ניתן להגיע למהירות המרבית V_max בכל ריכוז אנזים (מפאת התנהגותה האסימפטוטית של הפונקציה, מהירות התגובה V ממשיכה לגדול כשמוגדל ריכוז הסובסטרט [S]), אנזימים מאופיינים לרוב בריכוז הסובסטרט שבו קצב התגובה הוא חצי מהמהירות המקסימלית. ריכוז הסובסטרט נקרא קבוע מיכאליס-מנטן (K_m). קבוע זה מייצג (עבור תגובות אנזימטיות הפועלות על פי קינטיקת מיכאליס-מנטן פשוטה) את קבוע הדיסוציאציה של תצמיד האנזים-סובסטרט (ES). ערכים נמוכים מצביעים על כך שתצמיד האנזים-סובסטרט קשור יחדיו בחוזקה ומתפרק לעיתים רחוקות לפני שהסובסטרט עובר תחילה תגובה להפיכתו לתוצר.

משוואה

מ"מיכאליס-מנטן" הסיקו בריגס והולדן את התיאור הבא:

התגובה האנזימטית אמורה להיות בלתי הפיכה והתוצר לא נקשר מחדש לאנזים.

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle E + S \begin{matrix} \leftrightharpoons \end{matrix} [ES] \begin{matrix} \\ \longrightarrow\\ \ \end{matrix} E + P }

כיוון שאנו עוקבים אחר קירוב של המצב היציב (Steady state), ניתן להניח שהריכוזים של המתווכים לא משתנים, קרי נגזרות הזמן שלהם שוות לאפס:

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \frac{d[ES]}{dt} = k_1[E][S] - k_{3}[ES] - k_2[ES] = 0}

${\displaystyle [ES]={\frac {k_{1}[E][S]}{k_{-1}+k_{2}}}}$

את קבוע מיכאליס-מנטן ניתן להגדיר בצורה הבאה:

${\displaystyle K_{m}={\frac {k_{2}+k_{1}}{k_{3}}}}$

זה מפשט את צורת המשוואה ל: עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle [ES] = \frac{[E][S]}{K_m}} (1)

הריכוז הכולל של אנזים הוא סך האנזים החופשי בתמיסה ושל האנזים הקשור לסובסטרט, וריכוז האנזים החופשי נגזר מ:

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ [E_0] = [E] + [ES]}

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ [E] = [E_0] - [ES]} (2)

באמצעות ריכוז זה (2) וריכוז האנזים הקשור (1) אנו יכולים לרשום:

${\displaystyle [ES]={\frac {([E_{0}]-[ES])[S]}{K_{m}}}}$

ומכאן לסדר:

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle [ES] \frac{K_m}{[S]} = [E_0] - [ES]}

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle [ES]\left(1 + \frac{K_m}{[S]}\right) = [E_0]}

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle [ES] = [E_0]\frac{1}{1+\frac{K_m}{[S]}}} (3)

קצב הריאקציה הוא:

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \frac{d[P]}{dt} = k_2[ES]} (4)

בהצבת 3 ב-4 והכפלת המונה והמכנה בריכוז הסובסטרט [S] מתקבל:

${\displaystyle {\frac {d[P]}{dt}}=k_{2}[E_{0}]{\frac {[S]}{K_{m}+[S]}}=V_{max}{\frac {[S]}{K_{m}+[S]}}}$

המשוואה ניתנת לניתוח ניסיוני באמצעות גרף ליינוויבר בורק.

• E₀ היא הכמות ההתחלתית או הכוללת של האנזים. לא מעשי למדוד את כמות תצמיד האנזים-סובסטרט במהלך תגובה, כך שהתגובה צריכה להיכתב במונחים של כמות כוללת של אנזים, שהיא מידה ידועה.
• d[P]/dt ידוע גם כ-V₀ או קצב תגובה הוא קצב היווצרות התוצר.
• k₂[E₀] או V_max הוא קצב מקסימלי או מהירות מקסימלית. K₂ נקרא לעיתים k_cat.

כאשר ריכוז הסובסטרט [S] גדול באופן משמעותי מקבוע מיכאליס-מנטן K_m, [S]/(K_m + [S]) קרוב ל-1. לפיכך קצב היווצרות התוצר במקרה זה שווה ל-k₂[E₀].