שיטה איטרטיבית

דוגמה לשיטה איטרטיבית היא שיטת ניוטון-רפסון. מציאת השורש של הפונקציה (בכחול) נעשית באמצעות סדרת קירובים תוך שימוש במשיק (באדום)

במתמטיקה חישובית, שיטה איטרטיבית היא שיטה מתמטית שמשתמשת בניחוש התחלתי כדי לייצר סדרת קירובים טובים יותר ויותר לפתרון בעיה נתונה, כאשר הקירוב ה-n-י מחושב על ידי הקירובים שלפניו. שיטה איטרטיבית נקראת מתכנסת אם סדרת הפתרונות שהיא מייצרת מתכנסת לפתרון מסוים עבור קירוב ראשוני (כלומר עבור קלט מסוים). בדרך כלל תועדף שיטה בעלת התכנסות מוכחת, למרות זאת נפוץ השימוש גם בשיטות איטרטיביות שמשתמשות ביוריסטיקה (שכן למרות שהן לא מספקות ביטחון להתכנסות, הן מהירות יותר בדרך כלל).

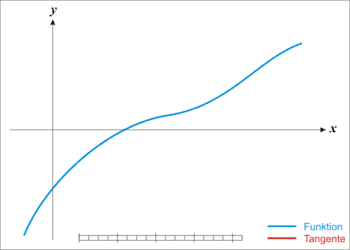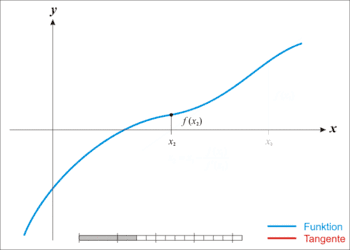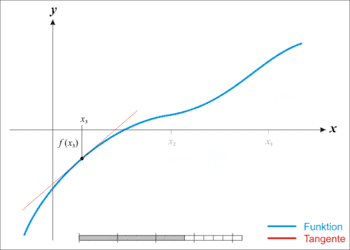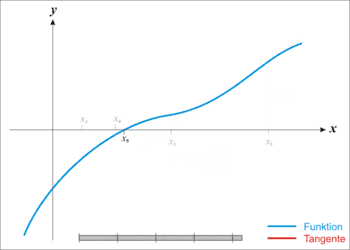
דוגמה מוכרת לשיטה איטרטיבית היא אלגוריתם למציאת שורשים של פונקציה (או מערכת משוואות), כדוגמת שיטת ניוטון-רפסון, המשתמשת בניחוש ראשוני כדי לייצר סדרת קירובים לפתרון. שיטה איטרטיבית נבדלת משיטה ישירה, שבה הבעיה נפתרת באמצעות סדרת פעולות סופית. בהיעדר שגיאות עיגול, שיטות ישירות צפויות להחזיר את הפתרון המדויק (כדוגמת פתרון מערכת משוואות $A\mathbf {x} =\mathbf {b}$ באמצעות שיטת החילוץ של גאוס). במקרים רבים שיטות איטרטיביות הן השיטות היחידות לפתרון לבעיה ובפרט במערכות משוואות לא ליניאריות. שיטות איטרטיביות שימושיות גם במערכות ליניאריות מרובות משתנים (לעיתים עם מיליוני משתנים) שבהן שיטות ישירות עשויות להיות יקרות לחישוב.

קישורים חיצוניים

ראו מדיה וקבצים בנושא זה בוויקישיתוף.

הערך באדיבות ויקיפדיה העברית, קרדיט,
רישיון cc-by-sa 3.0

This article is issued from Hamichlol. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.