אינטרפולציה לינארית
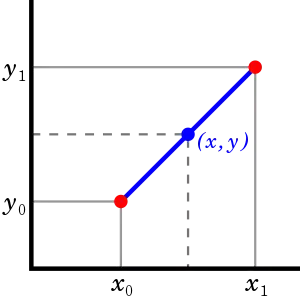
במתמטיקה, אינטרפולציה לינארית היא שיטה של התאמת עקומה תוך שימוש בפולינום לינארי כדי לבנות נקודות חדשות בטווח של נקודות נתונים בדידות ידועות.
אינטרפולציה לינארית בין שתי נקודות ידועות
אם שתי נקודות ידועות ניתנות על ידי הקואורדינטות ו , האינטרפונט הלינארי הוא קו ישר בין נקודות אלה. עבור ערך x במרווח את הערך y לאורך קו ישר ניתן למצוא על ידי המשוואה:
אשר יכול להיות נגזר גאומטרית מן האיור משמאל. זהו מקרה מיוחד של אינטרפולציה פולינומית עם n = 1.
פתרון המשוואה עבור y, כאשר ידוע ערך x, נותן:
וזו הנוסחה של אינטרפולציה לינארית במרווח . מחוץ למרווח זה, הנוסחה זהה לאקסטרפולציה.
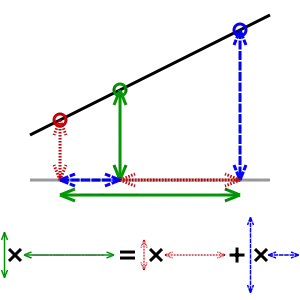
נוסחה זו יכולה גם להיות מובנת כממוצע משוקלל. המשקלים תלויים ביחס הפוך למרחק בין נקודות הקצה לנקודה ידועה; לנקודה קרובה יותר יש השפעה רבה יותר מאשר לנקודה רחוקה. לפיכך, המשקולות הם ו אשר הן מרחקים מנורמלים בין הנקודה הלא ידועה, ונקודות הקצה הידועות. מכיוון שאלו נסכמות ל-1:
אשר מניב את נוסחת האינטרפולציה הלינארית הנתונה לעיל.
אינטרפולציה של קבוצת נתונים
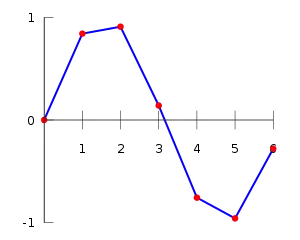
אינטרפולציה לינארית על קבוצה של נקודות נתונים מוגדר כשרשור אינטרפולנטים לינאריים בין כל זוג של נקודות נתונות. התוצאה היא עקומה רציפה, בדרך כלל עם נגזרת בלתי-רציפה, היינו פונקציה חלקה - .
אינטרפולציה לינארית כקירוב
אינטרפולציה לינארית משמשת לעיתים קרובות כדי לאמוד ערך של פונקציה מסוימת f באמצעות שני ערכים ידועים של הפונקציה בנקודות אחרות. השגיאה של קירוב זה מוגדרת:
כאשר p מציין את פולינום האינטרפולציה הלינארית שהוגדר לעיל
ניתן להוכיח באמצעות משפט רול שאם ל- f נגזרת שנייה רציפה, השגיאה תחומה על ידי:
כפי שרואים מכך, קירוב בין שתי נקודות עבור פונקציה נתונה מחמיר עם הנגזרת השנייה של פונקציה המקורבת. זה נכון גם באופן אינטואיטיבי: ככל שהפונקציה "עקומה" יותר, כך יורעו ההערכות שנעשות עם אינטרפולציה לינארית פשוטה.
יישומים
אינטרפולציה לינארית משמשת לעיתים קרובות כדי למלא פערים בטבלה. נניח שיש טבלה שמכילה אוכלוסיית ארץ מסוימת ב-1970, 1980, 1990 ו-2000, ורוצים להעריך את האוכלוסייה ב-1994. אינטרפולציה לינארית היא דרך קלה לעשות את זה.
הפעולה הבסיסית של אינטרפולציה לינארית בין שני ערכים נפוצה בגרפיקה ממוחשבת. בז'רגון, פעולה זו נקראת lerp. המונח יכול לשמש פועל או שם עצם של הפעולה.
פעולות lerp בנויות לתוך החומרה של כל מעבד גרפי במחשב מודרני. הן משמשות לעיתים קרובות בתור אבני בניין עבור פעולות מורכבות יותר: לדוגמה, אינטרפולציה בילינארית ניתן להשיג בשלושה lerpים. מכיוון שפעולה זו "זולה" (מבחינת ביצועים), זה גם דרך טובה ליישם טבלאות חיפוש מדויקות עם חיפוש מהיר עבור פונקציה חלקה מבלי לבצע יותר מדי דגימות של ערכי הטבלה.
הרחבות
דיוק
אם פונקציית C0 אינה מספיקה, למשל אם התהליך הזה הפיק נקודות נתונים הידועות כחלקות יותר מ - C0, מקובל להחליף אינטרפולציה לינארית עם "אינטרפולציית שֶׁגֶם" (spline interpolation), או אפילו אינטרפולציה פולינומית במקרים מסוימים.
רב משתנים
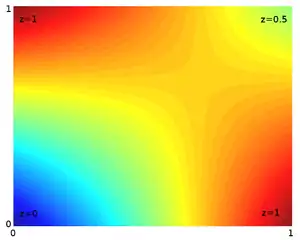
אינטרפולציה לינארית כפי שמתוארת כאן היא עבור נקודות נתונים בממד המרחבי הבודד. במקרה של שני ממדים מרחביים, הרחבה של אינטרפולציה לינארית נקרא אינטרפולציה בילנארית, בשלושה ממדים, אינטרפולציה תרילינארית. יש לשים לב, כי אינטרפולנטים אלו כבר אינם פונקציות לינאריות של קואורדינטות מרחביות, אלא תוצרים של פונקציות לינאריות; תופעה זו של איבוד לינאריות באה לידי ביטוי בבירור באיור שלמטה של אינטרפולציה בילנארית. הרחבות אחרות של אינטרפולציה לינארית יכולות להיות מיושמות בסוגים אחרים של רשת (mesh) , כגון רשת משולשת או טטראהדרלית, כולל "משטח בזייר" (Bézier surface). אלה עשויים להיות מוגדרים כפונקציה לינארית רב ממדית (האיור התחתון).
ראו גם
קישורים חיצוניים
- אינטרפולציה לינארית באינטרנט חישוב והדמיה כלי
- משוואות הקו הישר על Cut-the-knot
- יישום אינטרפולציה לינארית ב-Microsoft Excel
- Hazewinkel, מיכאל, אד. (2001), "אינטרפולציה לינארית", אנציקלופדיה של המתמטיקה, ספרינגר, ISBN 978-1-55608-010-4
- Hazewinkel, מיכאל, אד. (2001), "סופי-במרווחים נוסחה", אנציקלופדיה של המתמטיקה, ספרינגר, ISBN 978-1-55608-010-4
- לראות OrangeOwlSolutions על CUDA מימושים של אינטרפולציה לינארית.
- APLJaK אינטרפולציה לינארית מחשבון אחד מני רבים מחשבונים זמינים.