פונקציה לינארית למקוטעין

במתמטיקה, פונקציה לינארית למקוטעין היא פונקציה ממשית אשר מורכבת רק מהדבקת פונקציות לינאריות על המספרים הממשיים או חלק מהם. כאשר הפונקציה היא רציפה, אז הגרף שלה הוא עקומת מצולעים.

באופן מדויק יותר, עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f} היא לינארית למקוטעין אם קיימת חלוקה של הישר הממשי לקטעים זרים (יכולים להיות סגורים, פתוחים או סגורים רק באחד משני הקצוות) כך ש:

1. איחוד כל הקטעים הוא כל הישר הממשי: עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \biguplus_{\lambda\in\Lambda}I_\lambda=\R} .
2. בכל קטע ${\displaystyle I_{\lambda }}$ הפונקציה היא מהצורה ${\displaystyle y=a_{\lambda }x+b_{\lambda }}$ .

דוגמאות

פונקציה לינארית למקוטעין לדוגמה

קירוב של עקומה על ידי פונקציה לינארית למקוטעין

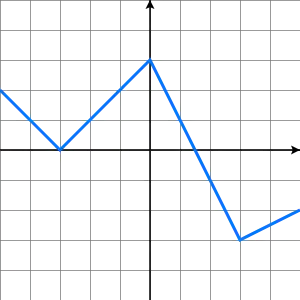
דוגמה לפונקציה לינארית למקוטעין היא הפונקציה:

${\displaystyle f(x)={\begin{cases}-x-3&:x\leq -3\\x+3&:-3<x<0\\-2x+3&:0\leq x<3\\0.5x-4.5&:x\geq 3\end{cases}}}$

הפונקציה הזו היא בעלת 4 חלקים (גרף עליון משמאל), והיא פונקציה רציפה המוגדרת לכל מספר ממשי.

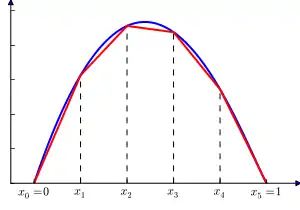
דוגמאות נוספות הן פונקציית רצפה, ערך מוחלט, גל שן מסור וכדומה. ניתן להשתמש בפונקציה לינארית למקוטעין בשביל לקרב פונקציה או עקומה כלשהי, כפי שניתן לראות בשרטוט התחתון משמאל. ישנם אלגוריתמים שיכולים לעשות זאת.