אלגברה לא אסוציאטיבית

מחלקות חשובות של אלגבראות לא אסוציאטיביות. חץ ממחלקה A למחלקה B פירושו שכל אלגברה מטיפוס A היא גם B. בכחול - האלגבראות הקומוטטיביות

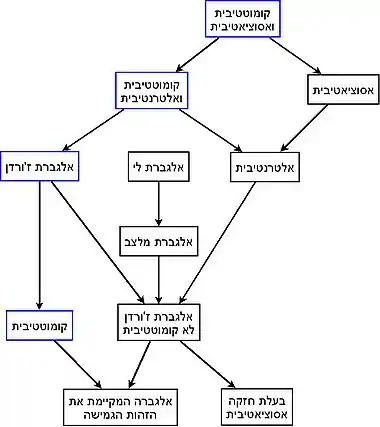
אלגברה לא אסוציאטיבית היא מבנה אלגברי דומה לאלגברה, למעט העובדה שאינו כולל דרישה לאקסיומת האסוציאטיביות (תכונת האסוציאטיביות עשויה להתקיים, כמובן, גם כאשר היא אינה נדרשת על-פי האקסיומות, ולכן כל אלגברה אסוציאטיבית היא סוג של "אלגברה לא אסוציאטיבית"). במלים אחרות, אלגברה לא אסוציאטיבית היא חוג לא אסוציאטיבי ${\displaystyle \ A}$ שבמרכזו חוג קומוטטיבי ${\displaystyle \ C}$.

אלגבראות לי, אלגבראות ז'ורדן ואלגבראות אלטרנטיביות כולן משפחות חשובות של אלגבראות לא אסוציאטיביות. בכל אחד מן המקרים האלה מניחים אקסיומות אחרות במקום אקסיומת האסוציאטיביות.

הגרעין והמרכז

הגרעין (nucleus) של אלגברה לא אסוציאטיבית A כולל את כל האיברים g המקיימים עיבוד הנוסחה נכשל (שגיאת המרה. השרת ("https://en.wikipedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle \ (g,x,y)=(x,g,y)=(x,y,g)=0} לכל x,y, כאשר ${\displaystyle \ (\cdot ,\cdot ,\cdot )}$ הוא האסוציאטור. זוהי תת-אלגברה אסוציאטיבית של A. המרכז מוגדר, כמו במקרה האסוציאטיבי, כאוסף האיברים של הגרעין, המתחלפים עם כל האיברים ב-A. אידאל האסוציאטור הוא האידאל הנוצר על ידי האיברים ${\displaystyle \ (x,y,z)}$, כלומר ${\displaystyle \ D(A)=A(A,A,A)A}$. זהויות המתקיימות בכל אלגברה לא אסוציאטיבית^[1] מבטיחות שהאידאל שווה ל- ${\displaystyle \ (A,A,A)+(A,A,A)A=(A,A,A)+A(A,A,A)}$.

אלגברת הפעולות

באלגברה לא אסוציאטיבית A, פעולת הכפל משמאל באיבר x מגדירה הומומורפיזם של מרחבים וקטוריים ${\displaystyle \ L_{x}:A\rightarrow A}$, על ידי ${\displaystyle \ L_{x}(y)=xy}$. זהו איבר של אלגברת ההומומורפיזמים עיבוד הנוסחה נכשל (שגיאת המרה. השרת ("https://en.wikipedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle \ \operatorname {End} (A)} , שהיא כמובן אסוציאטיבית. בדרך כלל (למשל, כאשר ל-A יש איבר יחידה), ההעתקה עיבוד הנוסחה נכשל (שגיאת המרה. השרת ("https://en.wikipedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle \ x\mapsto L_{x}} היא חד-חד-ערכית (השומרת כפל בדיוק כאשר A אסוציאטיבית). באופן דומה מוגדרת הפעולה של כפל מימין: ${\displaystyle \ R_{x}(y)=yx}$.

את האקסיומות המגדירות מחלקות שונות של אלגבראות לא-אסוציאטיביות אפשר לנסח, בדרך-כלל, בשפה של הפעולות מימין ומשמאל. לדוגמה, A אסוציאטיבית אם ורק אם ${\displaystyle \ L_{x}R_{y}=R_{y}L_{x}}$ לכל x,y. אלגבראות אלטרנטיביות מוגדרות לפי האקסיומות עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ L_x^2 = L_{x^2}} ו- ${\displaystyle \ R_{x}^{2}=R_{x^{2}}}$, בעוד שאלגבראות ז'ורדן הן אלו המקיימות ${\displaystyle \ R_{x}=L_{x}}$ (היינו, קומוטטיביות), ו- ${\displaystyle \ [L_{x},R_{x^{2}}]=0}$ (כאשר עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ [\cdot,\cdot]} הוא הקומוטטור של אופרטורים).

הזהות ${\displaystyle \ L_{x}R_{x}=R_{x}L_{x}}$ (כלומר, ${\displaystyle \ x(yx)=(xy)x}$ לכל x ו-y) נקראת זהות הגמישות, והיא מתקיימת ברוב המחלקות החשובות של אלגבראות לא-אסוציאטיביות, לרבות אלגבראות לי, ז'ורדן, ואלגבראות אלטרנטיביות.

מכיוון שתורת המבנה של אלגבראות אסוציאטיביות מפותחת יותר, ככלל, מזו של אלגבראות לא אסוציאטיביות, יש ערך למבנים אסוציאטיביים שאפשר לשייך לאלגברה לא אסוציאטיבית. הדוגמה החשובה ביותר למבנה כזה הוא אלגברת הפעולות, הנוצרת (כתת-אלגברה אסוציאטיבית של עיבוד הנוסחה נכשל (שגיאת המרה. השרת ("https://en.wikipedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle \ \operatorname {End} (A)} ) על ידי פעולות הכפל מימין ומשמאל. אלגברת הפעולות היא נילפוטנטית אם ורק אם A כזו. אם A אלגברה פשוטה או פשוטה למחצה, גם אלגברת הפעולות כזו, והכיוון ההפוך נכון בכל האלגבראות האלטרנטיביות.

אלגברת הנגזרות

את האלגברה של הנגזרות הפורמליות של A, היינו אוסף ההעתקות שומרות החיבור עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ D : A \rightarrow A} המקיימות את הזהות עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ D(ab)=aD(b)+D(a)b} , מסמנים ב-עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ \operatorname{Der}(A)} . זוהי תת-אלגברת לי של עיבוד הנוסחה נכשל (שגיאת המרה. השרת ("https://en.wikipedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle \ \operatorname {End} (A)} . נגזרת נקראת פנימית, אם היא שייכת לאלגברת-לי הנוצרת על ידי הפעולות עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ L_x, R_x} . ידוע שבמאפיין אפס, כל נגזרת של אלגברה פשוטה למחצה מממד סופי, עם יחידה ימנית או שמאלית, היא פנימית.

אלגברה לא אסוציאטיבית עם חילוק

לעומת המקרה האסוציאטיבי, במקרה הלא אסוציאטיבי יש הבדל בין הפיכות (נקודתית) של איבר לבין קיום פתרונות למשוואה מהצורה ${\displaystyle ax=b}$ (כאשר ${\displaystyle a\neq 0}$).

לכן, מגדירים אלגברה לא אסוציאטיבית עם חילוק בתור אלגברה לא אסוציאטיבית המקיימת את אחד התנאים השקולים הבאים:

• לכל עיבוד הנוסחה נכשל (שגיאת המרה. השרת ("https://en.wikipedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle a\neq 0,b} קיימים ויחידים עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle x,x'} כך ש-${\displaystyle ax=b,x'a=b}$.
• לכל עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a \neq 0 } אופרטורי הכפל משמאל ומימין, ${\displaystyle L_{a},R_{a}}$, הפיכים (בתור אופרטורים).

כמו במקרה האסוציאטיבי, אלגברה עם חילוק היא תחום (כלומר - אין מחלקי אפס), ובממד סופי כל תחום הוא אלגברת חילוק.

מכפלה טנזורית

אפשר להגדיר מכפלה טנזורית של שתי אלגבראות לא אסוציאטיביות - התוצאה היא תמיד אלגברה לא אסוציאטיבית, אבל לא בהכרח מאותה משפחה. לדוגמה, המכפלה של שתי אלגבראות אסוציאטיביות היא אלגברה אסוציאטיבית, אבל המכפלה של שתי אלגבראות ז'ורדן בדרך כלל אינה אלגברת ז'ורדן.

כמו במקרה האסוציאטיבי, המכפלה הטנזורית של אלגבראות לא אסוציאטיביות פשוטות מרכזיות גם היא פשוטה מרכזית.

ראו גם

• אלגברת לי, אלגברת מלצב
• אלגברה אלטרנטיבית
• אלגברת ז'ורדן
• אלגברה עם חזקה אסוציאטיבית
• רדיקל

לקריאה נוספת

הערות שוליים