אפקט סניאק

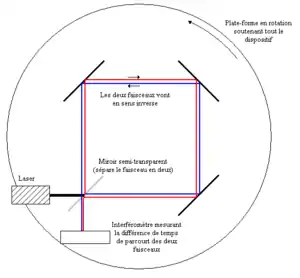
האינטרפרומטר של סניאק. אלומת אור מפוצלת לשתי אלומות אור שסובות את הלולאה בכיוונים מנוגדים ומתאבכות ביציאה. האינטרפומטר מותקן על שולחן מסתובב. נוסחת סניאק קובעת את הקשר בין הזזת המופע בהתאבכות לבין מהירות הסיבוב.

האינטרפרומר של סניאק^[1] הוא אינטרפרומטר טבעתי בו קרן אור בכניסה מפוצלת לשתי קרנים שסובבות לולאה בכוונים מנוגדים, ראה ציור. הפרש הפאזה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Delta \Phi} בין שתי האלומות נמדד בנקודת הכניסה לאחר ששתי האלומות השלימו סיבוב. כאשר האינטרפרומטר נמצא על משטח שמסתובב במהירות זוייתית עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Omega} , הפרש הפאזה בין שני הגלים קשור עם מהירות הסיבוב הזוויתית $\omega$ בנוסחת סניאק:

\Delta \Phi \approx {\frac {4\omega }{c^{2}}}{\boldsymbol {\Omega }}\cdot \mathbf {A}

כאשר $\mathbf {A}$

הוא השטח שמוגדר על ידי לולאת האינטרפרומטר ו- $\omega$ היא תדירות האור. לאינטרפרומטר שימושים רבים. השימוש החשוב ביותר הוא כגירוסקופ במערכות ניווט אינרציאליות. העקרון בבסיס הפעולה של אינטרפרומטר Sagnac נמצא בגירוסקופ לייזר טבעתי (Ring Laser Gyro)^[2] (ידוע גם בשם FOG-Fiber Optics Gyro).

היסטוריה

ג'ורג' סניאק פיתח את האינטרפרומטר שקרוי על שמו במטרה לבדוק את השערת האתר^[3]. האינטרפרומטר מבוסס על האינטרפרומטר הטבעתי של ארמן איפוליט פיזו. סניאק גזר את הנוסחה שנקראת על שמו בהנחה שמהירות האור היא c במערכת המעבדה, והסיק מכך, בטעות, שהניסיון מוכיח קיום מערכת מועדפת בה מהירות האור היא c ולכן מאשש את השערת האתר. למרות שהנוסחה אכן נכונה הפירוש שנתן לה סניאק שגוי: לפי תורת היחסות מהירות האור היא c בכל מערכת אינרציאלית, ולכן גם בקירוב בתוך מערכת המעבדה. סניאק כנראה לא הכיר או לא קבל את תורת היחסות הפרטית למרות שזו פורסמה 8 שנים קודם לכן ולמרות העובדה ששנתיים לפני כן מקס פון לאואה נתן הסבר תאורטי של האפקט במסגרת תורת היחסות^[4].

סניאק ערך את נסיונותיו כאשר המסלול של הקרן היה באוויר. נוסחת סניאק תקפה גם כאשר המסלול האופטי עובר דרך תווך דיאלקטרי שבו מהירות האור היא c/n כאשר $n>1$ הוא מקדם השבירה. הזזת הפאזה באינטרפרומטר של סניאק אינה תלויה במקדם השבירה בניגוד למשל להזזת הפאזה באינטרפרומטר של פיזו, שכן תלויה במקדם השבירה.

פיתוחים מאוחרים

בוריאציות מודרניות של האינטרפרומטר מזינים את שתי האלומות לסיב אופטי^[5]. השימוש החשוב ביותר של האינטרפרומטר הוא כגירוסקופ^[6]. הוא משמש גם חיישן טמפרטורה^[7] וחיישן עיבור^[8].

אפקט סניאק אינו ייחודי לאור, והוא תופעה כללית בגלים. הקבוע עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle c^2} שמופיע בנוסחת סניאק אינו קשור עם מהירות הגל אלא עם מבנה מרחב-זמן כמרחב מינקובסקי. אפקט דומה לסניאק קיים באלקטרונים כאפקט גלי של מכניקה קוונטית^[9].

האינטרפורמטר של וואנג. סיב אופטי גמיש נע כמו מסוע. מקור האור והגלאי נעים יחד עם הסיב. במקרה זה תקפה נוסחת סניאק המוכללת.

בשנת 2004 חקרו וואנג ושותפיו^[10]^[11] אינרפרומטרים טבעתיים עם סיב אופטי גמיש בתנועה של מסוע שאינה סיבוב קשיח^[12]. נוסחת סניאק המקורית אינה תקפה במקרה זה אבל ביטוי שקול שלה בנוסחה שתקרא להלן נוסחת סניאק-וואנג נמצא תקף נסיונית:

\Delta \Phi \approx {\frac {2\omega }{c^{2}}}\oint \mathbf {v} \cdot d\mathbf {x}

נוסחת סניאק ונוסחת סניאק-וואנג תקפות לסדר ראשון במהירות. נוסחה מדויקת במסגרת תורת היחסות היא^[13]

\Delta \Phi ={\frac {2\omega }{c^{2}}}\oint \gamma ^{2}\mathbf {v} \cdot d\mathbf {x}

גזירת אלמנטרית של נוסחת סניאק-וואנג^[14]

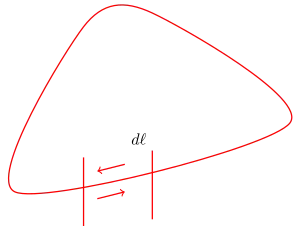
לולאה של סיב אופטי. שני החצים מציינים גלים שנעים בכוונים מנוגדים. אינטרול קטן של שסיב מסומן בעזרת עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle d\ell}

במערכת אינרציאלית רגעית הצמודה למקטע קטן של הסיב עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle d\mathbf{x}'} שארכו במערכת העצמיתעיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle d\ell'=|d\mathbf{x}'|} , (ראה ציור), הזמן שלוקח לאור לעבור את המקטע אינו תלוי בכיוון התקדמות הגל ונקבע על ידי מהירות האור בסיב

dt'_{\pm }={n \over c}d\ell '

האורך העצמי והאורך במעבדה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle d\ell} קשורים זה בזה על ידי נוסחת התכווצות האורך עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle d\ell'=\gamma d\ell\approx d\ell} כאשר הזהות המקורבת היא עד לסדר שני במהירות יחסית למהירות האור. במערכת המעבדה הזמן שלוקח לאור לעבור את המקטע תלוי בכיוון הגל ונתון בנוסחת טרנספורמציות לורנץעיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle dt_\pm=\gamma \left(dt' \pm \frac{\mathbf{v}\cdot d\mathbf{x}'}{c^2}\right) \approx \frac n c d\ell \pm \frac{\mathbf{v}\cdot d\mathbf{x}}{c^2}} כאשר רמת הדיוק היא לסדר ראשון במהירות. הזמן שלוקח לאור להקיף את הסיב תלוי בכוון התפתחות הגל. וגלים שהגיעו לגלאי באותו זמן, יצאו בהפרש זמנים מהליזרעיבוד הנוסחה נכשל (שגיאת המרה. השרת ("https://en.wikipedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle \Delta T=\int \left(dt_{+}-dt_{-}\right)\approx {\frac {2}{c^{2}}}\oint \mathbf {v} \cdot d\mathbf {x} } הפרש הזמנים מתורגם להפרש מופע

\Delta \Phi \approx {\frac {2\omega }{c^{2}}}\oint \mathbf {v} \cdot d\mathbf {x}

זו הנוסחה הכללית של סניאק-וואנג לסיב שנע בתנועה כללית (ללא מתיחה). כאשר הסיב נע כגוף קשיח עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\textstyle \mathbf{v}=\boldsymbol{\omega}\times\mathbf{x}} ובמקרה זה ניתן לבטא את האינטגרל באמצעות השטח שהלולאה מגדירה:

\oint \mathbf {v} \cdot d\mathbf {x} =\oint {\boldsymbol {\omega }}\times \mathbf {x} \cdot d\mathbf {x} =\oint {\boldsymbol {\omega }}\cdot \mathbf {x} \times d\mathbf {x} =2{\boldsymbol {\omega }}\cdot \int d\mathbf {A} =2{\boldsymbol {\omega }}\cdot \mathbf {A}

הצבה בנוסחת סניאק-וואנג נותנת את נוסחת סניאק המקורית.

קישורים חיצוניים

ראו מדיה וקבצים בנושא זה בוויקישיתוף. על אפקט סניאק, באתר MathPages (באנגלית)

הערות שוליים

↑ Sagnac, Georges (1913), "Sur la preuve de la réalité de l'éther lumineux par l'expérience de l'interférographe tournant" [On the proof of the reality of the luminiferous aether by the experiment with a rotating interferometer], Comptes Rendus, 157: 1410–1413
↑ W. W. Chow, J. Gea-Banacloche, L. M. Pedrotti, V. E. Sanders, W. Schleich, and M. O. Scully, The ring laser gyro, Rev. Mod. Phys. 57, 61, 1985.
↑ Sagnac, Georges (1913), "L'éther lumineux démontré par l'effet du vent relatif d'éther dans un interféromètre en rotation uniforme" [The demonstration of the luminiferous aether by an interferometer in uniform rotation], Comptes Rendus, 157: 708–710
↑ Max von Laue, Über einen Versuch zur Optik der bewegten Körper ., Münchener Sitzungsberichte: 405–412
↑ H. J. Arditty and H. C. Lefevre, Sagnac effect in fiber gyroscopes, Opt. Lett. 6, 401, 1981.
↑ R. Anderson, H. R. Bilger, and G. E. Stedman, Sagnac effect: A century of earth rotated interferometers, Am. J. Phys. 62, 975 (1994).
↑ D. M. Shupe, Thermally induced nonreciprocity in the fiberopticinterferometer, Appl. Opt. 19, 654 (1980).
↑ X. Dong, H. Y. Tam, and P. Shum, Temperature-insensitive strain sensor with polarization-maintaining photonic crystal fiber based sagnac interferometer, Appl. Phys. Lett. 90, 151113 (2007).
↑ F. Hasselbach and M. Nicklaus, Sagnac experiment with electrons: Observation of the rotational phase shift of electron waves in vacuum, Phys. Rev. A 48, 143 (1993).
↑ E. J. Post, Sagnac effect, Rev. Mod. Phys. 39, 475 (1967).
↑ G. B. Malykin, The Sagnac effect: Correct and incorrect explanations, (Phys. Usp. 43, 1229 (2000.
↑ Wang, R.; Zheng, Y.; Yao, A.; Langley, D (2006). "Modified Sagnac experiment for measuring travel-time difference between counter-propagating light beams in a uniformly moving fiber". Physics Letters A. 312: 7–10. arXiv:physics/0609222 . doi:10.1016/S0375-9601(03)00575-9.
↑ J. Avron and O. Kenneth, Relativistically exact eikonal equation for optical fibers with application to adiabatically deforming ring interferometers, Physical Review A 94, 063838, 2016
↑ ِA. Ori and J. Avron, Generalized Sagnac-Wang-Fizeau formula, Phys. Rev. A 94, 063837, 2016

הערך באדיבות ויקיפדיה העברית, קרדיט,
רישיון cc-by-sa 3.0

This article is issued from Hamichlol. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Sagnac, Georges (1913), "Sur la preuve de la réalité de l'éther lumineux par l'expérience de l'interférographe tournant" [On the proof of the reality of the luminiferous aether by the experiment with a rotating interferometer], Comptes Rendus, 157: 1410–1413

[2] W. W. Chow, J. Gea-Banacloche, L. M. Pedrotti, V. E. Sanders, W. Schleich, and M. O. Scully, The ring laser gyro, Rev. Mod. Phys. 57, 61, 1985.

[3] Sagnac, Georges (1913), "L'éther lumineux démontré par l'effet du vent relatif d'éther dans un interféromètre en rotation uniforme" [The demonstration of the luminiferous aether by an interferometer in uniform rotation], Comptes Rendus, 157: 708–710

[4] Max von Laue, Über einen Versuch zur Optik der bewegten Körper ., Münchener Sitzungsberichte: 405–412

[5] H. J. Arditty and H. C. Lefevre, Sagnac effect in fiber gyroscopes, Opt. Lett. 6, 401, 1981.

[6] R. Anderson, H. R. Bilger, and G. E. Stedman, Sagnac effect: A century of earth rotated interferometers, Am. J. Phys. 62, 975 (1994).

[7] D. M. Shupe, Thermally induced nonreciprocity in the fiberopticinterferometer, Appl. Opt. 19, 654 (1980).

[8] X. Dong, H. Y. Tam, and P. Shum, Temperature-insensitive strain sensor with polarization-maintaining photonic crystal fiber based sagnac interferometer, Appl. Phys. Lett. 90, 151113 (2007).

[9] F. Hasselbach and M. Nicklaus, Sagnac experiment with electrons: Observation of the rotational phase shift of electron waves in vacuum, Phys. Rev. A 48, 143 (1993).

[10] E. J. Post, Sagnac effect, Rev. Mod. Phys. 39, 475 (1967).

[11] G. B. Malykin, The Sagnac effect: Correct and incorrect explanations, (Phys. Usp. 43, 1229 (2000.

[12] Wang, R.; Zheng, Y.; Yao, A.; Langley, D (2006). "Modified Sagnac experiment for measuring travel-time difference between counter-propagating light beams in a uniformly moving fiber". Physics Letters A. 312: 7–10. arXiv:physics/0609222 . doi:10.1016/S0375-9601(03)00575-9.

[13] J. Avron and O. Kenneth, Relativistically exact eikonal equation for optical fibers with application to adiabatically deforming ring interferometers, Physical Review A 94, 063838, 2016

[14] ِA. Ori and J. Avron, Generalized Sagnac-Wang-Fizeau formula, Phys. Rev. A 94, 063837, 2016