אקסצנטריות (מתמטיקה)

חתכי חרוט

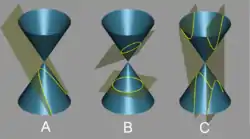
במתמטיקה, אקסצנטריות של חתך חרוט היא ערך מספרי המודד עד-כמה העקום רחוק מלהיות מעגל. בפרט,

• האקסצנטריות של מעגל היא 0.
• האקסצנטריות של אליפסה גדולה מ־0 וקטנה מ־1.
• האקסצנטריות של פרבולה היא 1.
• האקסצנטריות של היפרבולה גדולה מ־1.
• האקסצנטריות של קו ישר היא אינסוף.

לאקסצנטריות חשיבות גובהה מאד במכניקה מסלולית, מכיוון שתנועת גרמי שמים סביב השמש היא תמיד בחתכי חרוט; לפי החוק הראשון של קפלר תנועה של כוכב לכת היא אליפסה שהשמש נמצאת באחד המוקדים שלה.

אליפסה

אליפסה, עם סימון המוקדים, הצירים והאקסצנטריות הלינארית שלה

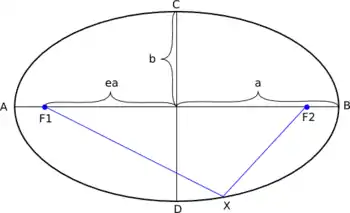
באליפסה, מגדירים אקסצנטריות כיחס בין מרחק המוקדים (${\displaystyle F_{1}}$ ו־${\displaystyle F_{2}}$) לבין הציר הראשי, כלומר: עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \left(\frac{\overline{F_1F_2}}{\overline{AB}}\right)} .

אם אורך חצי הציר הראשי של האליפסה הוא a, ואורך חצי הציר המשני שלה הוא b, האקסצנטריות נתונה בנוסחה: ${\displaystyle e={\sqrt {1-{\frac {b^{2}}{a^{2}}}}}}$.

לגבי אליפסה יש מדד נוסף שנקרא פחיסות המוגדר כ: עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f =\frac {a - b}{a}} . קיים קשר פשוט בין הפחיסות לבין אקסצנטריות של אליפסה או פני שטח הספרואיד על פי נוסחת המעבר: ${\displaystyle f=1-(1-e)^{1/2}}$ .

היפרבולה

אם אורך חצי הציר הראשי של ההיפרבולה הוא a, ואורך חצי הציר המשני שלה הוא b, האקסצנטריות נתונה בנוסחה: ${\displaystyle e={\sqrt {1+{\frac {b^{2}}{a^{2}}}}}}$ .

קישורים חיצוניים

• אקסצנטריות, באתר MathWorld (באנגלית)