היפרבולה
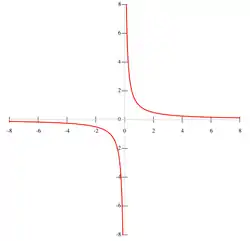
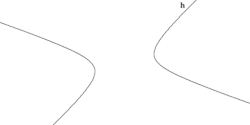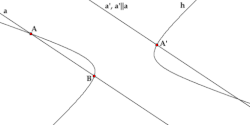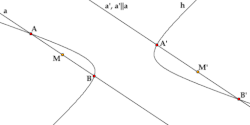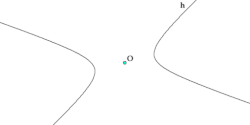
במתמטיקה, הִיפֶּרְבּוֹלָה היא צורה גאומטרית המהווה חתך חרוט, המורכבת משתי עקומות נפרדות הקרויות זרועות ההיפרבולה.
ההיפרבולה ניתנת להגדרה כמקום הגאומטרי של הנקודות שמקיימות שהערך המוחלט של ההפרש בין המרחקים שבין כל אחת מהן לשתי נקודות קבועות (נקודות המוקד) הוא קבוע.
ההיפרבולה ניתנת לייצוג על פני מערכת צירים קרטזית כעקומה, באמצעות המשוואה האלגברית הבאה:
כאשר .
ניתן להגדיר היפרבולה גם כמקום הגאומטרי של הנקודות שהיחס בין מרחקן מנקודה קבועה (מוקד) וישר נתון (מדריך) הוא קבוע גדול מ-1. קבוע זה הוא האקסצנטריות של ההיפרבולה.
אמצע הקטע שבין שני המוקדים נקרא מרכז ההיפרבולה. להיפרבולה שתי אסימפטוטות שנחתכות במרכזה. תהליך למציאת מרכז היפרבולה מתואר באנימציה.
היפרבולה בעלת צירים שווים נקראת היפרבולה שוות שוקיים. היפרבולה שמרכזה בראשית הצירים נקראת היפרבולה קנונית.
משוואות המתארות היפרבולה
מערכת קואורדינטות קרטזית
(המרכז (המוקד): עיבוד הנוסחה נכשל (שגיאת המרה. השרת ("https://en.wikipedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle (h,k)} )
- עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \begin{align}\frac{(x-h)^2}{a^2}-\frac{(y-k)^2}{b^2}&=1\\\frac{(y-k)^2}{a^2}-\frac{(x-h)^2}{b^2}&=1\end{align}}
בשתי משוואות אלה, הציר הראשי ו-עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle b} הציר המשני, אולם ייתכן ש-עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle b} יהיה גדול מ- .
במקרה הפרטי של היפרבולה קנונית (כלומר, שהמוקד נמצא בראשית הצירים – עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (0,0)} ), מתקבלת הנוסחה:
- עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \frac{x^2}{a^2}-\frac{y^2}{b^2}=1}
ניתן להבחין בדמיון הרב בין נוסחה זו לנוסחתה של אליפסה קנונית עיבוד הנוסחה נכשל (שגיאת המרה. השרת ("https://en.wikipedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1} .
האקסצנטריות נקבעת על פי המשוואה:
- עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle e=\sqrt{1+\frac{b^2}{a^2}}}
היפרבולה בה צירי הקואורדינטות זהים לצירי ההיפרבולה:
משוואות האסימפטוטות הן:
מערכת קואורדינטות קטבית
הצגה פרמטרית (לענף הימני)
תכונות אנליטיות של ההיפרבולה
השטח תחת ההיפרבולה
האינטגרל של ההיפרבולה "הפשוטה" מהצורה: עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle y^2-x^2=1} הוא:
- .
ניתן להגיע לתוצאה זאת באמצעות טכניקה אלגנטית של שינוי מערכת קואורדינטות מ-עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (x,y)} למערכת קואורדינטות המסובבת בזווית 45 מעלות ביחס למערכת הצירים ומקיימת עיבוד הנוסחה נכשל (שגיאת המרה. השרת ("https://en.wikipedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle y^{*}={\frac {C}{x^{*}}}} .
טרנספורמציית קואורדינטות זו מתאפשרת אודות לעובדה שהפונקציה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle y=\frac1x} היא למעשה היפרבולה, מה שמסביר את הופעת הלוגריתם בתוצאת האינטגרציה של השטח תחת ההיפרבולה (אינטגרל של הוא עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ln(x)} ). האבר הנוסף בתוצאה נובע מכך שהשטח תחת ההיפרבולה מורכב גם ממשולש ישר-זווית "שאריתי" שניצביו עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle x,\sqrt{1+x^2}} .
ראו גם
- זווית היפרבולית
- פונקציה היפרבולית
- מסלול היפרבולי
- מבנה היפרבולי