ארגומנט (אנליזה מרוכבת)

איור 1. תרשים ארגנד זה מייצג את המספרים המרוכבים הנמצאים על המישור. עבור כל נקודה במישור, ארגומנט (arg)  היא פונקציה אשר מחזירה את זווית φ.

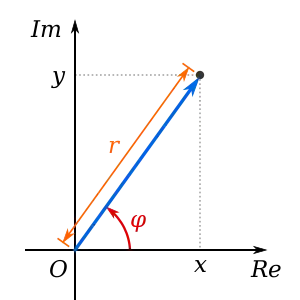
במתמטיקה, הארגומנט (Argument) הוא פונקציה רב-ערכית הפועלת על מספרים מרוכבים שאינם אפסיים. כשהמספר המרוכב z מייצג נקודה על המישור המרוכב, הארגומנט של z הוא זווית בין הציר הממשי החיובי והקו המחבר את נקודת המוצא, כפי שמוצג כ-φ באיור 1 ומסומן כ- arg z. כדי להגדיר פונקציה בעלת ערך אחד, נשתמש בערך העיקרי של הארגומנט (לפעמים מכונה Arg z). הוא נבחר להיות ערך ייחודי של הארגומנט הזה בקטע ${\displaystyle (-\pi ,+\pi ]}$.

הגדרה

באיור 2. מוצגות שתי אפשרויות לארגומנט: עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \varphi} ו-עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \varphi + 2\pi} . 

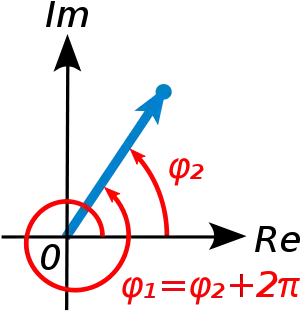
הארגומנט של המספר המרוכב ${\displaystyle z=x+iy\in \mathbb {C} -\{0\}}$, מכונה arg(z), מוגדר בשתי דרכים שוות ערך:

1. מבחינה גאומטרית, במישור המרוכב, כשהזווית φ חיובית מהציר הממשי עד הווקטור המייצג את z. הערך המספרי נתון על ידי הזווית ברדיאנים, והוא חיובי אם נמדד נגד כיוון השעון.
2. מבחינה אלגברית, כל מספר ממשי ${\displaystyle \varphi \in \mathbb {R} }$ שמקיים
   $${\displaystyle z=re^{i\phi }=r\cdot (\cos \varphi +i\sin \varphi )}$$

   
   עבור r חיובי ממשי (ראו הנוסחה של אוילר). הגודל ${\displaystyle r=|z|}$ הוא הערך המוחלט של z ולפעמים מכונה "מודולוס", גאומטרית זהו אורך הקו המחבר בין z לראשית הצירים (אורך הווקטור ${\displaystyle (x,y)\in \mathbb {R} ^{2}}$). הארגומנט, בעיקר בהקשרים פיזיקליים, מכונה לעיתים מופע (phase).

תחת שתי ההגדרות, ניתן לראות כי לארגומנט של כל מספר מרוכב שאינו אפס יש הרבה ערכים אפשריים: ראשית, בתור זווית הנדסית, זה ברור כי כל סיבוב מעגל שלם לא משנה את הנקודה, אז זוויות שונות על ידי הוספת מספר של 2π ברדיאנים (מעגל שלם) הם אותו הדבר, כפי שהיא באה לידי ביטוי על ידי איור 2 מימין. באופן דומה, מן מחזוריות של סינוס וקוסינוס, גם להגדרה השנייה יש את התכונה הזאת. הארגומנט של אפס בדרך כלל נשאר לא מוגדר.

הקשר בין הפונקציה הרב-ערכית של הארגומנט לערך העיקרי ("הענף הראשי") הוא עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{arg}(z) = \operatorname{Arg}(z) + 2 \pi \mathbb{Z} = \{ \operatorname{Arg}(z) + 2\pi n \mid n \in \mathbb{Z} \} }

ערך עיקרי

משום שהשלמת סיבוב סביב המקור משאיר מספר מרוכב ללא שינוי, ישנן אפשרויות רבות אשר לערך ש-φ יכול לקבל על ידי המקור בכל מספר שלם של פעמים. זה מוצג באיור 4, ייצוג של הפונקציה הרב ערכית (לערך נבחר)קו אנכי (לא מוצג באיור) חותך את השטח בגובה מייצג את כל האפשרויות של זווית על הנקודה הזו.

כאשר פונקציה מוגדרת היטב נדרשת אז הבחירה הרגילה, המכונה "הארגומנט הראשי" שהוא מקרה פרטי של ערך עיקרי או ענף ראשי. לשם כך יש להגדיר קטע פתוח-סגור באורך 2π שבו הארגומנט יכול לקבל ערכים. באנליזה מרוכבת מקובל לבחור בקטע החצי-סגור חצי-פתוח

$${\displaystyle I_{0}=(-\pi ,\pi ]=\{x\in \mathbb {R} \mid -\pi <x\leq \pi \}}$$

כקטע בו מוגדר הארגומנט הראשי. זה שקול לזווית שערכה נע בין פאי רדיאנים (כולל) למינוס פאי רדיאנים (לא כולל), במעלות זה שקול לזווית שנעה בין 180 מעלות (כולל) למינוס 180 מעלות (לא כולל). בטקסטים שונים בוחרים לעיתים בקטעים אחרים להגדרת הארגומנט הראשי, כגון עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle [0,2\pi]} .

חישוב מהחלק הממשי והמדומה

בהינתן ההגדרה הגאומטרית של הארגומנט, קל לראות שמציאת הארגומנט של ${\displaystyle z=x+iy\in \mathbb {C} }$ שקולה למציאת הזווית של ${\displaystyle (x,y)\in \mathbb {R} ^{2}}$ בקואורדינטות קוטביות.

אם בוחרים לעבוד באינטרוול עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ [ 0, 2 \pi )} , כלומר, הזווית מקבלת ערכים בין 0 ל-2π (לא כולל 2π), מוסכמה המקובלת באנליזה וקטורית, אזי ניתן למצוא את הזווית לפי הנוסחה הבאה:

${\displaystyle \ \varphi =\operatorname {atan1} \left({\tfrac {y}{x}}\right)={\begin{cases}\arctan({\frac {y}{x}})&{\mbox{if }}x>0{\mbox{ and }}y\geq 0\\\arctan({\frac {y}{x}})+2\pi &{\mbox{if }}x>0{\mbox{ and }}y<0\\\arctan({\frac {y}{x}})+\pi &{\mbox{if }}x<0\\{\frac {\pi }{2}}&{\mbox{if }}x=0{\mbox{ and }}y>0\\{\frac {3\pi }{2}}&{\mbox{if }}x=0{\mbox{ and }}y<0\end{cases}}}$

כאשר arctan היא הפונקציה ההופכית לפונקציה הטריגונומטרית טנגנס.

אם עובדים באינטרוול עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ (-\pi, \pi]} , המקובל יותר באנליזה מרוכבת, יש להשתמש בנוסחה הבאה:

${\displaystyle \ \varphi =\operatorname {atan2} \left({\tfrac {y}{x}}\right)={\begin{cases}\arctan({\frac {y}{x}})&{\mbox{if }}x>0\\\arctan({\frac {y}{x}})+\pi &{\mbox{if }}x<0{\mbox{ and }}y\geq 0\\\arctan({\frac {y}{x}})-\pi &{\mbox{if }}x<0{\mbox{ and }}y<0\\{\frac {\pi }{2}}&{\mbox{if }}x=0{\mbox{ and }}y>0\\-{\frac {\pi }{2}}&{\mbox{if }}x=0{\mbox{ and }}y<0\end{cases}}}$

הפונקציה המפוצלת הזאת נקראת לעיתים קרובות atan2 ("ארכטנגס 2") ורושמים עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \varphi = \operatorname{atan2}(y/x)} .

זהויות

אחד המניעים העיקריים עבור הגדרת הערך העיקרי Arg הוא היכולת לכתוב מספרים מרוכבים בצורת ערך מוחלט וארגומנט. לכן עבור כל מספר מרוכב מתקיים עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle z = |z| e^{i \arg(z)}=|z| e^{i \operatorname{Arg}(z)}} זה תקף רק אם עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle z \ne 0} אבל יכול להיחשב גם ב-z=0 אם קובעים ${\displaystyle \operatorname {Arg} (0)=c\in \mathbb {R} }$ (מספר ממשי סופי) באופן שרירותי (שימו לב ש-${\displaystyle |0|=0}$).

עוד כמה זהויות מתקדמות יותר עוקבות. אם ${\displaystyle z_{1},z_{2}\in \mathbb {C} ^{\times }=\mathbb {C} -\{0\}}$ הם שני מספרים מרוכבים שונים מאפס, אז

• עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{Arg}(z_1 z_2) \equiv \operatorname{Arg}(z_1) + \operatorname{Arg}(z_2) \pmod{(-\pi,\pi]}} ,
• עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{Arg}\biggl(\frac{z_1}{z_2}\biggr) \equiv \operatorname{Arg}(z_1) - \operatorname{Arg}(z_2) \pmod{(-\pi,\pi]}} .

אם z ≠ 0 ו-עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle n \in \mathbb{Z}} הוא כל מספר שלם, אז

• עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{Arg}\left(z^n\right) \equiv n \operatorname{Arg}(z) \pmod {(-\pi,\pi]}} .

לדוגמה:

${\displaystyle \operatorname {Arg} {\biggl (}{\frac {-1-i}{i}}{\biggr )}=\operatorname {Arg} (-1-i)-\operatorname {Arg} (i)=-{\frac {3\pi }{4}}-{\frac {\pi }{2}}=-{\frac {5\pi }{4}}}$

ביבליוגרפיה (מתורגמת מהערך באנגלית)

• Ahlfors, Lars (1979). Complex Analysis: An Introduction to the Theory of Analytic Functions of One Complex Variable (3rd ed.). New York;London: McGraw-Hill. ISBN 0-07-000657-1.
• Ponnuswamy, S. (2005). Foundations of Complex Analysis (2nd ed.). New Delhi;Mumbai: Narosa. ISBN 978-81-7319-629-4.
• Beardon, Alan (1979). Complex Analysis: The Argument Principle in Analysis and Topology. Chichester: Wiley. ISBN 0-471-99671-8.
• Borowoski, Ephraim; Borwein Jonathan (2002) [1st ed. 1989 as Dictionary of Mathematics]. Mathematics. Collins Dictionary (2nd ed.). Glasgow: HarperCollins. ISBN 0-00-710295-X.

קישורים חיצוניים

• ארגומנט, באתר MathWorld (באנגלית)