אנליזה וקטורית

וקטורים

וקטור במרחב וקטורי מממד סופי אפשר לכתוב בצורה ${\displaystyle {\vec {v}}=(v_{1},\ldots ,v_{n})}$ , כאשר ${\displaystyle v_{1},\ldots ,v_{n}}$ הם הרכיבים או הקואורדינטות של ${\displaystyle {\vec {v}}}$ .

במרחב התלת־ממדי הווקטורים ${\displaystyle {\hat {x}},{\hat {y}},{\hat {z}}}$ מייצגים את וקטורי הבסיס הסטנדרטי, המתאימים למערכת צירים קרטזית. בכתיבה לפי רכיבים, הם שווים לווקטורים ${\displaystyle (1,0,0),(0,1,0),(0,0,1)}$ בהתאמה.

למבוא יותר אינטואיטיבי על וקטורים במרחב התלת־ממדי, ראו וקטור (פיזיקה).

חיבור

חיבור וקטורים: מחברים וקטורים לפי רכיבים: ${\displaystyle (v_{1},\ldots ,v_{n})+(w_{1},\ldots ,w_{n})=(v_{1}+w_{1},\ldots ,v_{n}+w_{n})}$ .

כפל

בניגוד לחיבור, יש מספר סוגים של פעולות כפל המערבים וקטורים:

1. כפל בסקלר: אם ${\displaystyle c\in \mathbb {R} }$ הוא מספר ממשי ו־${\displaystyle {\vec {v}}}$ וקטור, אז ${\displaystyle c{\vec {v}}=(cv_{1},\ldots ,cv_{n})}$ הוא הכפל של ${\displaystyle v}$ בסקלר ${\displaystyle c}$ .
2. מכפלה סקלרית (Dot product): המכפלה הסקלרית של שני וקטורים היא מספר, המוגדר לפי ${\displaystyle (v_{1},\cdots ,v_{n})\cdot (w_{1},\cdots ,w_{n})=v_{1}w_{1}+\cdots +v_{n}w_{n}}$ . מספר זה הוא מכפלת האורך של הווקטור הראשון, האורך של הווקטור השני וקוסינוס הזווית שביניהם. כלומר ${\displaystyle {\vec {v}}\cdot {\vec {w}}=|{\vec {v}}||{\vec {w}}|\cos(\theta )}$ . המכפלה הסקלרית מתאפסת אם ורק אם הווקטורים ניצבים.
3. מכפלה וקטורית (Cross product): במרחב התלת־ממדי ${\displaystyle \mathbb {R} ^{3}}$ מוגדרת פעולה נוספת, הנקראת מכפלה וקטורית. המכפלה הווקטורית של שני וקטורים ${\displaystyle {\vec {v}},{\vec {w}}}$ היא וקטור המאונך לשניהם, שאורכו הוא כשטח המקבילית הנוצרת ביניהם, כלומר אורך הווקטור הראשון כפול אורך השני כפול סינוס הזווית שביניהם.

את כללי החישוב של המכפלה הווקטורית קל לזכור באמצעות סימון הדטרמיננטה:

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (v_1,v_2,v_3)\times(w_1,w_2,w_3)=\begin{vmatrix}\hat x&\hat y&\hat z\\v_1&v_2&v_3\\w_1&w_2&w_3\end{vmatrix}}

כאשר ${\displaystyle {\hat {x}},{\hat {y}},{\hat {z}}}$ הן וקטורי היחידה של הצירים X ,Y ,Z בהתאמה.

בעוד ששתי הפעולות הראשונות מוגדרות בכל ממד, ובפרט בממד־1 מתכנסות לכפל הרגיל, המכפלה הווקטורית מוגדרת רק במרחב האוקלידי מממד 3.

שדה סקלרי

פונקציה ${\displaystyle f:\mathbb {R} ^{n}\to \mathbb {R} }$ המתאימה לכל נקודה במרחב ערך סקלרי נקראת שדה סקלרי או בהשאלה מפיזיקה (ובייחוד אלקטרומגנטיות): פוטנציאל.

דוגמאות במרחב תלת־ממדי:

• טמפרטורת המים בנהר – לכל נקודה בנהר (המרחב) מותאמת הטמפרטורה באותה נקודה (סקלר).
• פוטנציאל חשמלי.
• עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f(x,y,z)=x^2+3yz^5-4ze^{x-y}}

שדה וקטורי

פונקציה ${\displaystyle {\vec {f}}:\mathbb {R} ^{n}\to \mathbb {R} ^{n}}$ המתאימה לכל נקודה במרחב וקטור (ליתר דיוק, וקטור מהמרחב המשיק באותה נקודה) נקראת שדה וקטורי.

דוגמאות במרחב תלת־ממדי:

• זרימת מים בנהר – לכל נקודה בנהר (המרחב) מותאם וקטור שכיוונו ככיוון זרימת המים באותה נקודה וגודלו כמהירות הזרימה.
• שדה חשמלי.
• עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \vec f(x,y,z)=\left(xy+42~,~56\sin(z)~,~e^{y^2-xz}\right)=(xy+42)\hat x+56\sin(z)\hat y+e^{y^2-xz}\hat z}

השדות בדרך כלל אינם לינאריים, ואפילו לא בהכרח רציפים. למרות זאת, באנליזה וקטורית מתעניינים בעיקר בפונקציות חלקות (שיש להן נגזרות מכל סדר), או בעלות מספר סופי בלבד של נקודות סינגולריות.

מבוא

האופרטור הבסיסי במרחב זה הוא אופרטור הגזירה (נקרא גם דֶל), המוגדר:

$${\displaystyle {\vec {\nabla }}\equiv {\hat {x}}{\frac {\partial }{\partial x}}+{\hat {y}}{\frac {\partial }{\partial y}}+{\hat {z}}{\frac {\partial }{\partial z}}\equiv (\partial _{x},\partial _{y},\partial _{z})}$$

אפשר לקבל את האופרטורים הדיפרנציאליים היסודיים על ידי פעולות הכפל השונות בהן משתתף אופרטור הגזירה:

1. הגרדיאנט של שדה סקלרי עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f} הוא שדה וקטורי ${\displaystyle {\vec {\nabla }}f}$ שרכיביו הם הנגזרות החלקיות של השדה המקורי.
2. הדיברגנץ של שדה וקטורי עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \vec f} הוא שדה סקלרי עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \vec\nabla\cdot\vec f} המודד את קצב השינוי במאונך לצירים.
3. הרוטור (או curl) של שדה וקטורי תלת־ממדי עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \vec f} הוא שדה וקטורי עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \vec\nabla\times\vec f} המודד את כיוון השינוי של השדה המקורי.

המכפלה הסקלרית של עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \nabla} עם עצמו היא אופרטור חשוב אחר, הנקרא לפלסיאן.

לעיתים נקרא הסימון המשולש של האופרטור בשם "נבלא" או "נבלה", על שום דמיונו לנבל (בתחביר LaTeX הוא מוצג על ידי הפקודה \nabla). בספרים רבים נהוג לכתוב את המשולש ההפוך של הדל בגופן (פונט) מודגש, במקום לרשום חץ קטן למעלה. מטרת שני הסימונים היא להדגיש שמדובר בווקטור.

גרדיאנט

המחשה של גרדיאנט. באיורים שלפנינו, השדה הסקלרי מתואר באמצעות שינוי הצבע, כאשר אזורים כהים יותר הם ערכים גדולים יותר של הפונקציה. החצים הכחולים מתארים את הגרדיאנט הנגזר מהשדה הסקלרי. שימו לב שהחצים פונים אל עבר האזורים הגבוהים יותר

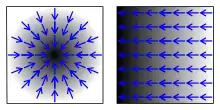
גרדיאנט הוא אופרטור המקבל פונקציה סקלרית (פונקציית פוטנציאל) ומחזיר פונקציה וקטורית שרכיביה הם הנגזרות החלקיות של הפונקציה המקורית.

המשמעות הגאומטרית של הגרדיאנט היא שהוא מחזיר את השינוי בפוטנציאל (השדה הסקלרי) כתוצאה מ"תזוזה" במרחב. מאחר שמדובר במרחב תלת־ממדי, הכיוון משפיע על השינוי של הפונקציה בנוסף לגודל התזוזה. הכיוון של הווקטור שמחזיר הגרדיאנט הוא הכיוון בו השינוי בפונקציה מקסימלי.

הגרדיאנט מוגדר באופן הבא:

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \text{grad}f(x,y,z)=\frac{\part f}{\part x}\hat x+\frac{\part f}{\part y}\hat y+\frac{\part f}{\part z}\hat z}

באמצעות אופרטור הדל, אפשר לרשום

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \text{grad}f=\vec\nabla f}

כלומר הפעלה של האופרטור הווקטורי דל על הפונקציה הסקלרית בצורה של כפל בסקלר, וקבלה של פונקציה וקטורית.

עבור כל שדה סקלרי, אופרטור הגרדיאנט מחזיר שדה וקטורי שנקרא "Gradient Field" ובו החצים מכוונים לכיוון בו הפונקציה עולה וגודלם של החצים מייצג את השיפוע של השדה הסקלרי. הכיוון של הגרדיאנט הוא הכיוון שבו יש שינוי מקסימלי בערך של הפונקציה.

דוגמה פיזיקלית: הפוטנציאל האלקטרוסטטי מסומן ${\displaystyle \phi }$ , מחוקי האלקטרוסטטיקה ידוע לנו כי ${\displaystyle {\vec {E}}=-{\vec {\nabla }}\phi }$ כאשר E הוא השדה החשמלי.

דיברגנץ

הדיברגנץ הוא מעין מדד לכמות השטף של שדה וקטורי היוצא מנקודה כלשהי במרחב.

רוטור (Curl)

הרוטור הוא גודל דיפרנציאלי המודד את נטייתו של שדה וקטורי להסתובב סביב נקודה מסוימת.

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \text{curl}\vec F=\lim_{a_i\to0}\frac{1}{a_i}\oint_{c_i}(\vec F\cdot d\vec r)\cdot\hat{n}_i}

כאשר עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_i} מסמל גודל של משטחונים המחלקים שטח פנים של נפח מסוים, ${\displaystyle c_{i}}$ מסמל את העקומים התוחמים כל אחד ממשטחונים אלו ו־עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \hat{n}_i} מסמל את וקטורי היחידה המאונכים למשטחונים אלו.

ניתן להראות שבקאורדינטות קרטזיות הרוטור ניתן לחישוב על ידי מכפלה וקטורית של האופרטור דל בשדה:

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \text{curl}\vec F=\vec\nabla\times\vec F=\left(\frac{\part F_z}{\part y}-\frac{\part F_y}{\part z}\right)\hat x+\left(\frac{\part F_x}{\part z}-\frac{\part F_z}{\part x}\right)\hat y+\left(\frac{\part F_y}{\part x}-\frac{\part F_x}{\part y}\right)\hat z}

צורת רישום קלה יותר לזכירה של הנוסחה לעיל היא באמצעות הדטרמיננטה של המטריצה הבאה:

${\displaystyle {\vec {\nabla }}\times {\vec {F}}=\det {\begin{bmatrix}{\hat {x}}&{\hat {y}}&{\hat {z}}\\{\frac {\partial }{\partial x}}&{\frac {\partial }{\partial y}}&{\frac {\partial }{\partial z}}\\F_{x}&F_{y}&F_{z}\end{bmatrix}}}$

בתנאי שמפתחים לפי השורה הראשונה. יש להדגיש כי זהו סימון שגוי מבחינה מתמטית (שהרי אופרטור גזירה אינו יכול להיות אבר במטריצה).

צורה אחרת היא באמצעות סימן לוי-צ'יוויטה:

עיבוד הנוסחה נכשל (שגיאת המרה. השרת ("https://en.wikipedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle {\vec {\nabla }}\times {\vec {F}}=\epsilon _{ijk}{\hat {e}}_{i}(\partial _{j}F_{k})}

כאשר ${\displaystyle \epsilon _{xyz}=1}$ ושומר סימן לכל תמורה ציקלית של האינדקסים, הופך סימן עבור תמורה אי-זוגית של האינדקסים ומקבל את הערך 0 אם יש שני אינדקסים זהים. כמו כן,

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \part_j:=\frac{\part}{\part r_j}}

הוא סימון מקוצר לנגזרת החלקית (למשל: עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \part_{r_1}=\part_{r_x}=\part_x} היא גזירה לפי x כאשר y ו־z מוחזקים כקבועים).

לפלסיאן

הלפלסיאן הכללי מוגדר בקואורדינטות קרטזיות:

${\displaystyle \nabla ^{2}={\frac {\partial ^{2}}{\partial x^{2}}}+{\frac {\partial ^{2}}{\partial y^{2}}}+{\frac {\partial ^{2}}{\partial z^{2}}}}$

כיוון שזהו אופרטור סקלרי הוא יכול לפעול הן על פונקציה סקלרית (על ידי כפל סימבולי רגיל משמאל), והן על פונקציה וקטורית (על ידי כפל בסקלר סימבולי משמאל).

אינטגרל קווי

אינטגרל משטחי

באנליזה וקטורית ישנם שני סוגי אינטגרל משטחי:

1. אינטגרל משטחי מסוג ראשון:

   אינטגרל של שדה סקלרי: ${\displaystyle \int _{S}f({\vec {r}})dS}$

2. אינטגרל משטחי מסוג שני:

   אינטגרל של שדה וקטורי: ${\displaystyle \int _{S}{\vec {F}}({\vec {r}})\cdot d{\vec {S}}=\int _{S}{\vec {F}}({\vec {r}})\cdot {\hat {n}}\,dS}$

כאשר ${\displaystyle d{\vec {S}}={\hat {n}}\,dS}$ הוא וקטור משטח אינפיניטסימלי שגודלו כגודל השטח האיפיניטסימלי וכיווני ניצב למשטח (הווקטור עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \hat n} הוא וקטור יחידה נורמל הניצב למשטח.

אינטגרל רב-ממדי