זרימה פוטנציאלית

תיאור ומאפיינים

זרימה פוטנציאלית מורכבת על ידי סופרפוזיציה של זרימות פשוטות

קווי זרם של זרימה פוטנציאלית בלתי דחיסה מסביב לגליל בזרימה מציפה.

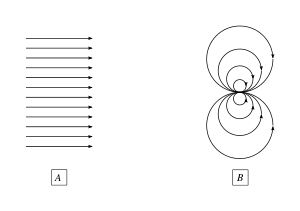
בדינמיקת זורמים זרימה פוטנציאלית מתוארת על ידי פונקציית פוטנציאל φ שבמקרה הכללי היא פונקציה של המרחב והזמן. מהירות הזרימה מתוארת על ידי השדה הווקטורי v ששווה לגרדיאנט של פונקציית הפוטנציאל.^[1]

${\displaystyle V=\nabla \varphi }$

יש המגדירים לפעמים את המהירות בצורה הבאה:

${\displaystyle V=-\nabla \varphi }$

אבל אנחנו נשתמש בהגדרה הראשונה (ללא המינוס).

מחשבון וקטורי ניתן לקבל שהרוטור של הגרדיאנט שווה לאפס^[1]

${\displaystyle \nabla \times \nabla \varphi =0}$

וכתוצאה מכך מתקבל שהערבוליות (שהיא הרוטור של שדה המהירות שווה לאפס גם כן:^[1]

${\displaystyle \nabla \times V=0}$

משתמע מכך שזרימה פוטנציאלית היא זרימה אי-רוטציונית.

לתוצאה זו יש השלכות ישירות עבור המקרים שבהם ניתן (או לא ניתן) ליישם זרימה פוטנציאלית. באזורים בזרימה שבהם ידוע שהערבוליות חשובה, כמו שבלים במים או שכבות גבול, הזרימה הפוטנציאלית לא מצליחה לספק תחזיות סבירות על הזרימה.^[2] למזלנו ישנם אזורים רבים בשדה זרימה שבהם ההנחה של זרימה אי רוטציונית תקפה, ובשל כך נעשה שימוש בזרימה פוטנציאלית ביישומים רבים, למשל: בזרימות מסביב כנף דקה, בעיות אקוסטיות, גלי מים ובזרימה אלקרטו - אוסמוטית.^[3]

זרימה בלתי דחיסה

עבור המקרה של זרימה בלתי דחיסה - למשל עבור נוזל, או גז במספרי מאך נמוכים, אבל לא עבור גלי קול - דיברגנץ המהירות שווה לאפס^[1]

${\displaystyle \nabla \cdot V=0}$

כתוצאה מכך מתקבל שפונקציית פוטנציאל המהירות צריכה לקיים את משוואת לפלס^[1]

${\displaystyle \nabla ^{2}\varphi =0}$

כאשר ${\displaystyle \nabla \cdot \nabla =\nabla ^{2}}$ הוא הלפלסיאן (לעיתים מסומן ב - Δ). במקרה זה הזרימה נקבעת באופן מוחלט מהקינמטיקה שלה, כלומר מההנחות של שדה אי רוטציוני ושהדיברגנץ של המהירות הוא אפס. הדינמיקה של הבעיה יכולה להיות מחושבת לאחר מכן אם אנו מעוניינים בחישוב לחצים, לדוגמה עבור זרימה מסביב לכנף דקה (ואגב כך חישוב כח העילוי, למשל שיעבוד על הכנף) על ידי שימוש בעקרון ברנולי. עבור המקרה הדו-ממדי, הבעיה של זרימה פוטנציאלית מצטמצמת לבעיה מאד פשוטה שמנותחת על ידי שימוש באנליזה קומפלסקית (פירוט בהמשך הערך).

זרימה דחיסה

זרימה תמידית

זרימה פוטנציאלית יכולה לשמש על מנת למדל זרימה דחיסה אי רוטציונית. פונקציית הפוטנציאל המלאה המארת זרימה במצב מתמיד נתונה ע"י:^[4]

${\displaystyle (1-M_{x}^{2}){\frac {\partial ^{2}\phi }{\partial x^{2}}}+(1-M_{y}^{2}){\frac {\partial ^{2}\phi }{\partial y^{2}}}+(1-M_{z}^{2}){\frac {\partial ^{2}\phi }{\partial z^{2}}}-2M_{x}M_{y}{\frac {\partial ^{2}\phi }{\partial x\partial y}}-2M_{y}M_{z}{\frac {\partial ^{2}\phi }{\partial y\partial z}}-2M_{z}M_{x}{\frac {\partial ^{2}\phi }{\partial z\partial x}}=0}$

כאשר רכיבי מספר מאך הם: ${\displaystyle M_{z}={\frac {1}{a}}{\frac {\partial \phi }{\partial z}}}$, ${\displaystyle M_{y}={\frac {1}{a}}{\frac {\partial \phi }{\partial y}}}$, ${\displaystyle M_{x}={\frac {1}{a}}{\frac {\partial \phi }{\partial x}}}$

כאשר a היא מהירות הקול הלוקאלית.

מהירות הזורם במקרה זה גם כן שווה ל - ${\displaystyle \nabla \phi }$, כאשר Φ היא פונקציית פוטנציאל המהירות. פונקציית הפוטנציאל המלאה תקפה עבור זרימה תת-קולית, קולית, ועל קולית, בזווית התקפה כלשהי, כל עוד שההנחה של זרימה אי רוטציונית נשמרת. עבור המקרה של זרימה תת-קולית או על-קולית בזוויות התקפה קטנות ועבור גופים דקים, ניתן להניח הנחה נוספת: ניתן לפצל את פוטנציאל המהירות לזרימה מציפה בלתי מופרעת בכיוון X: ${\displaystyle V_{\infty }}$, ומהירות מופרעת קטנה ${\displaystyle \nabla \varphi }$ לכן:^[4]

${\displaystyle \nabla \phi =V_{\infty }X+\nabla \varphi }$

עבור מקרה זה המשוואה הלינארית (שעברה לינאריזציה) עבור הפרעות קטנות של הפוטנציאל - שהיא קירוב למשוואה הפוטנציאלית המלאה - ניתנת לכתיבה: ${\displaystyle (1-M_{\infty }^{2}){\frac {\partial ^{2}\varphi }{\partial x^{2}}}+{\frac {\partial ^{2}\varphi }{\partial y^{2}}}+{\frac {\partial ^{2}\varphi }{\partial z^{2}}}=0}$

כאשר ${\displaystyle {\frac {V_{\infty }}{a_{\infty }}}=M_{\infty }}$ הוא מספר המאך של הזרימה המציפה. המשוואה הלינארית הרבה יותר פשוטה למימוש וניתן לצמצמה למשוות לפלס על ידי הנחנה שהגודל האופייני בכיוון X גדול בהרבה יותר מאשר בכיוונים האחרים.

גלי קול

ערכים ראשיים : קול, אקוסטיקה, משוואת הגלים.

ניתן לקרב גלי קול בעלי אמפליטודה נמוכה על ידי מודל זרימה פטנציאלית^[5] בצורה הבאה: ${\displaystyle {\frac {\partial ^{2}\varphi }{\partial t^{2}}}={\bar {a}}\nabla ^{2}\varphi }$ שהיא משוואת גלים לינארית לגבי פוטנציאל המהירות φ. החלק האוסצילטורי של וקטור המהירות V קשור לפוטנציאל המהירות על ידי ${\displaystyle V=\nabla ^{2}\varphi }$ כאשר ${\displaystyle {\bar {a}}}$ היא מהירות הקול הממוצעת בתווך הומוגני. נשים לב שגם החלקים האוסצילטורים של הלחץ P והצפיפות ρ מקיימים באופן עצמאי את משוואת הגלים בקירוב זה.

יישומיות ומגבלות

זרימה פוטנציאלית לא כוללת בתוכה את כל המאפיינים שזרימות שונות כוללות בתוכן בעולם האמיתי. למשל, זרימה פוטנציאלית לא כוללת בתוכה טורבולנציה, שהיא צורה שכיחה של זרימה בטבע. בנוסף, זרימה פוטנציאלית לא יכולה לתאר זרימות פנימיות צמיגות.^[2] מזרימה פוטנציאלית גם מתקבלות כמה תחזיות שלא תואמות את המציאות, כמו פרדוקס ד'למבר, שאומר שכח הגרר שפועל על גוף נח בשדה זרימה אינסופי הוא אפס. (פרדוקס זה ייושב על ידי הצגת הרעיון של שכבות גבול). או אם נדייק, זרימה פוטנציאלית לא לוקחת בחשבון התנהגות של זרימות שכוללות בתוכן שכבות גבול.^[2] למרות זאת, הבנה של זרימה פוטנציאלית חשובה בהרבה ענפים של מכניקת זורמים. במיוחד זרימות פוטנציאליות פשוטות (נקראות זרימות אלמנטריות) כמו, ערבול או מקור\בור אשר קיים עבורם פתרון אנליטי סגור. את הפתרונות הללו ניתן לשלב על ידי עקרון הסופרפוזיציה על מנת ליצור זרימות יותר מסובכות אשר מקיימות מגוון של תנאי שפה שונים (כמו למשל מידול של השפעת פיצוץ על קיר ועוד). בנוסף, זרימות אלו תואמות (אף על פי שלעיתים לא במדויק) זרימות בחיים האמיתיים בכל התחומים של מכניקת זורמים ; בנוסף, ניתן לקבל תובנות רבות וחשובות כאשר מתחשבים בסטייה (שלפעמים יכולה להיות קטנה מאד) בין תצפיות של זרימה והזרימה הפוטנציאלית התואמת. ישנם יישומים רבים של זרימה פוטנציאלית למשל בעיצוב מטוסים. לדוגמה, בדינמיקת זורמים חישובית טכניקה אחת היא לחבר פתרון של זרימה פוטנציאלית מחוץ לשכבת הגבול לפתרון לשדה הזרימה בתוך שכבת הגבול. התוצאה של היעדר שכבות גבול היא שניתן להחליף כל קו זרם בקו של חומר לכאורה ללא הפרעה לשדה הזרימה, וזאת מכיוון שהתאוריה הפוטנציאלית מזניחה את השפעות החיכוך (שנגרם עקב צמיגותו של הזורם) מה שמתברר כהנחנה טובה לרוב שדה הזרימה חוץ מבתוך שכבת הגבול.

הערות כלליות

ניתן להציב ב -f כל פונקציה דיפרנציאבילית. בדוגמאות הבאות נשתמש במגוון של פונקציות אלמנטריות ; ניתן להתמש גם בפונקציות מיוחדות. נשים לב כי פונקציות שאינן חד-חד-ערכיות כמו הלוגריתם הטבעי גם כן ניתנות למימוש, אבל צריכים להגביל אותן למשטח רימן אחד.

התנהגות חזקות

במקרה שחזקות מופעלות על המפה הקונפורמית מעבירים את ${\displaystyle z=x+iy}$ ל עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle w = \varphi +i\psi} ^[7]:

${\displaystyle w=Az^{n}}$

לאחר מכן על ידי כתיבה של z בקואורדינטות פולריות ${\displaystyle z=x+iy=re^{i\theta }}$ נקבל^[7]

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \psi = Ar^nsin(n\theta)} ו ${\displaystyle \varphi =Ar^{n}cos(n\theta )}$

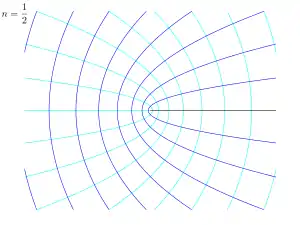
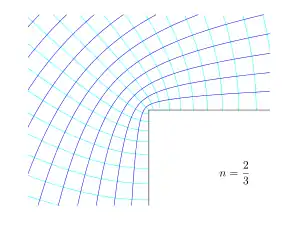
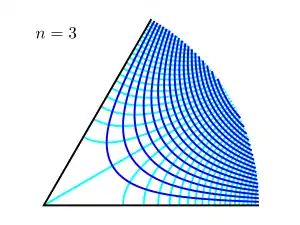
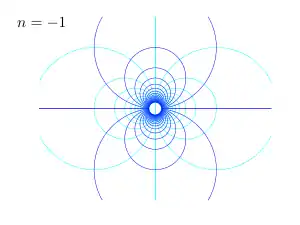
באיורים משמאל ניתן לראות דוגמאות עבור ערכים שונים של n, הקווים השחורים מתארים את גבולות הזרימה (פינה, משטח אופקי וכו'), הקווים הכחולים הכהים מתארים את קווי הזרם והקווים הכחולים הבהירים את הקווים שווי הפוטנציאל. כמה חזקות מעניינות כתלות ב-n^[7]:

- ${\displaystyle n={\frac {1}{2}}}$ : מתאר זרימה סביב משטח חצי אינסופי.

- עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle n = \frac{2}{3}}  : מתאר זרימה ליד פינה ימנית.

- עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle n = 1}  : מקרה טריוויאלי של זרימה מציפה.

- ${\displaystyle n=2}$ : זרימה היוצאת מפינה או נקודת סטגנציה.

- ${\displaystyle n=-1}$ : זרימה הנוצרת כתוצאה מזוגן.

הקבוע A הוא פרמטר אשר מתאר את עוצמת הזרימה כאשר עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle |A|} מתאר את העוצמה, בעוד שהארגומנט עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle arg[A]} מייצג רוטציוניות (במידה ואינה אפס).

התנהגות חזקות עבור n = 1 זרימה מציפה

אם ${\displaystyle w=Az^{1}}$ כלומר, n=1, קווי הזרם (כלומר הקווים שעליהם ${\displaystyle \psi =const}$ ) מהווים מערכת של קווים ישרים המקבילים לציר x. קל לראות זאת על ידי פירוק לרכיבים ממשיים ומרוכבים:

עיבוד הנוסחה נכשל (שגיאת המרה. השרת ("https://en.wikipedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle f(x+iy)=A(x+iy)=Ax+iAy}

מכאן ש - עיבוד הנוסחה נכשל (שגיאת המרה. השרת ("https://en.wikipedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle \varphi =Ax} ו עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \psi = Ay} , זרימה זו נקראת זרימה מציפה בכיוון x.

התנהגות חזקות עבור n = 2

אם ${\displaystyle n=2}$ אז ${\displaystyle w=Az^{2}}$ וקווי הזרם המתאימים לערך קבוע מסוים של ${\displaystyle \psi }$ מקיימים את המשוואה:

${\displaystyle \psi =Ar^{2}sin(2\theta )}$

אשר מתארת מערכת של קווים היפרבולים. ניתן להראות זאת על ידי פירוק לרכיבים (ממשיים ומרוכבים), נשים לב ש - עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle sin(2\theta) = 2cos(\theta)sin(\theta)} ובהצבה של עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle sin(\theta) = \frac{y}{r}} ו ${\displaystyle cos(\theta )={\frac {x}{r}}}$ ניתן להראות (אחרי פישוט) שהמשוואה המתארת את קווי הזרם היא:

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \psi = 2Axy}

שדה המהירות נתון על ידי ${\displaystyle \nabla \varphi }$ או :

${\displaystyle {\begin{pmatrix}u\\v\end{pmatrix}}={\begin{pmatrix}{\frac {\partial \varphi }{\partial x}}\\{\frac {\partial \varphi }{\partial y}}\end{pmatrix}}={\begin{pmatrix}{\frac {\partial \psi }{\partial y}}\\-{\frac {\partial \psi }{\partial x}}\end{pmatrix}}={\begin{pmatrix}2Ax\\-2Ay\end{pmatrix}}}$

בדינמיקת זורמים שדה הזרימה ליד מקור תואם זרימה ליד נקודת סטגנציה. נשים לב שהזורם במקור נמצא במנוחה (מתקבל מההגדרה שהנגזרת של ${\displaystyle f(z)=z^{2}}$ ב ${\displaystyle z=0}$ ). קו הזרם שבו עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \psi = 0} מעניין במיוחד מכיוון שיש לו שני (או ארבעה) ענפים אשר עוקבים אחרי הצירים כלומר ${\displaystyle x=0}$ ו ${\displaystyle y=0}$. מכיוון ששום זורם לא זורם על ציר x, נוכל להתייחס אליו כאל גבול מוצק. ולכן אפשר להתעלם המזרימה בחצי המישור השלילי עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle y < 0} ולהתרכז בזרימה בחצי המישור העליון. עם תובנה זו ניתן לדמות את זרימה זו לזרימה שנוצרת כתוצאה מהטזת סילון מים אנכי על מישור אופקי. ניתן גם לדמות את הזרימה כזרימה ליד פינה ישרה (עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 90^0} ) אם מסתכלים על האזור בו ${\displaystyle x>0}$ וגם עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle y > 0} .

התנהגות חזקות עבור n = 3

אם n = 3 הזרימה המתקבלת דומה לזרימה עבור n = 2 רק שכאן הזווית של הפינה שווה ל - עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 60^0} . קווי הזרם:

${\displaystyle \psi =3x^{2}y-y^{2}}$

התנהגות חזקות עם n = -1 זוגן

אם n = -1 קווי הזרם נתונים על ידי:

${\displaystyle \psi =-{\frac {A}{r}}sin(\theta )}$

ובפירוק לרכיבים:

${\displaystyle \psi =-{\frac {Ay}{r^{2}}}=-{\frac {Ay}{x^{2}+y^{2}}}}$

${\displaystyle x^{2}+y^{2}+{\frac {Ay}{\psi }}=0}$

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle x^2 + (y + \frac{A}{2\psi})^2 = (\frac{A}{2\psi})^2}

ולכן קווי הזרם הם מעגלים אשר ניצבים לציר ה - x בגובה של המקור. המעגלים בחצי המישור העליון זורמים ביכוון השעון והמעגלים בחצי המישור התחתון נגד כיוון השעון. נשים לב שרכיבי המהירות פרופורציונלים ל - עיבוד הנוסחה נכשל (שגיאת המרה. השרת ("https://en.wikipedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle r^{-2}} ושהערכים שלהם במקור הם אינסופיים. לצורת הזרימה קוראים זוגן וניתן לדמות זוגן על ידי מקור ובור בעוצמה מסוימת אשר ממוקמים במרחק אינפינטיסימלי קטן זה מזה. שדה המהירות נתון על ידי: עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (u,v) = (\frac{\partial \psi}{\partial y} , -\frac{\partial \psi}{\partial x}) = (A\frac{y^2 - x^2}{(x^2 + y^2)^2} , -A\frac{2xy}{(x^2 + y^2)^2})}

ובקואורדינטות פולריות:

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (u_r, u_\theta) = (\frac{1}{r}\frac{\partial\psi}{\partial \theta}, -\frac{\partial \psi}{\partial r}) = (-\frac{A}{r^2}cos\theta,-\frac{A}{r^2}sin\theta)}

התנהגות חזקות עם ${\displaystyle n=-2}$ quadrupole

אם n = -2 קווי הזרם הם:

${\displaystyle \psi =-{\frac {A}{r^{2}}}sin(2\theta )}$

זרימה זו נקראת quadrupole.