חתכי דדקינד

המחשה גאומטרית של חתך דדקינד המתאים ל־2√. עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle A} קבוצת הרציונליים בתחום האדום ו-${\displaystyle B}$ קבוצת הרציונליים בתחום הכחול

חתכי דדקינד מהווים אחת משתי השיטות הקלאסיות לבנייה של שדה המספרים הממשיים מתוך שדה המספרים הרציונליים. אלו הן הבניות הראשונות של שדה זה שאינן תלויות באקסיומות גאומטריות. את הבניה הציג ריכרד דדקינד ב-1872. באותה שנה הציע גאורג קנטור את הבניה באמצעות "סדרות קושי".

חתך במספרים הרציונליים הוא חלוקה שלהם לשתי קבוצות לא-ריקות ${\displaystyle A,B}$ , כך שכל איבר של עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle A} קטן מכל איבר של ${\displaystyle B}$ , וכך של-עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle A} אין מקסימום. למשל, אם עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle r} הוא מספר רציונלי, אפשר לבחור

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle A=\{x:x<r\},B=\{x:x\ge r\}}

אז עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle A|B} הוא החתך המתאים ל-עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle r} . חתכים אלה, שאותם אפשר לאפיין גם בכך שלקבוצה ${\displaystyle B}$ יש מינימום, נקראים "החתכים הרציונליים".

אפשר להגדיר פעולות חיבור וכפל בין חתכים, והאוסף המתקבל הוא שדה, שאוסף החתכים הרציונליים מהווה תת-שדה שלו. יתרה מזו, קל לסדר את השדה החדש (עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle A|B} גדול מ-עיבוד הנוסחה נכשל (שגיאת המרה. השרת ("https://en.wikipedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle A'|B'} אם עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle A} מכיל את עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle A'} ), ואז השיכון של הרציונליים בשדה החתכים (המתאים לכל מספר רציונלי את החתך שלו) שומר על יחס הסדר.

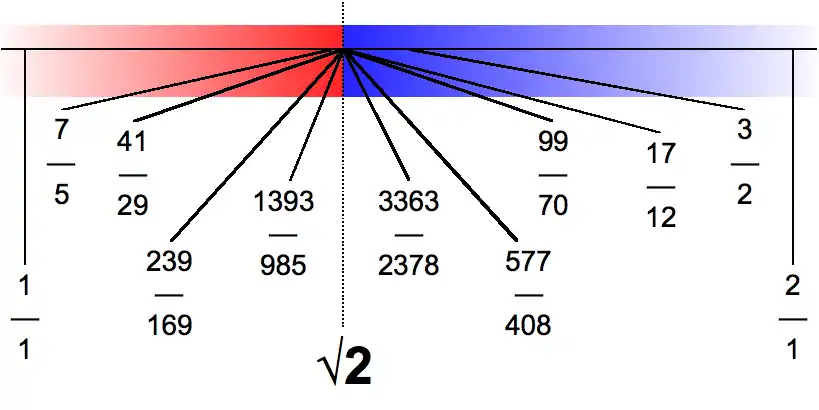
ישנם גם חתכים אי-רציונליים. למשל, אפשר לקחת את ${\displaystyle B}$ להיות קבוצת המספרים הרציונליים החיוביים, שריבועם גדול מ-2, ואת עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle A} להיות המשלים של ${\displaystyle B}$ . במקרה זה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle A|B} הוא חתך שריבועו שווה לחתך המתאים ל-2, ולכן אינו יכול להיות רציונלי (שהרי השורש הריבועי של 2 אינו רציונלי).

מתברר שהשדה החדש הוא שדה סדור שלם ארכימדי, והוא השדה היחיד בעל תכונות אלה. לשדה זה קוראים שדה המספרים הממשיים. את אוסף החתכים אפשר לבנות עבור כל שדה סדור, אלא שהתוצאה אינה שדה אלא אם השדה המקורי הוא ארכימדי. אוסף החתכים בשדה ארכימדי איזומורפי בכל המקרים לשדה המספרים הממשיים.

ב-1972 הכליל את הרעיון ג'ון הורטון קונוויי, ובנה את מה שכונה אחר-כך מספרים סוריאליסטיים.