מודל מרקוב חבוי

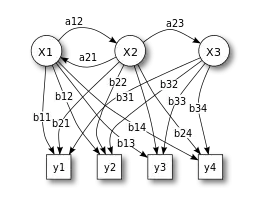
מודל מרקוב חבוי: העיגולים בשורה העליונה (x) מציינים מצבים נסתרים מעיני הצופה, הריבועים בשורה התחתונה מציינים אותיות הפלט (y), החצים המסומנים ב-a מציינים הסתברויות מעבר בין מצבים וכאלו המסומנים ב-b מייצגים הסתברות לפלט

מודל מרקוב חבוי (Hidden Markov model; ובקיצור HMM) הוא מודל סטוכסטי המאפשר למדל מערכת כתהליך מרקובי עם מצבים חבויים (כאלו שאינם ידועים לצופה).

הבסיס המתמטי והאלגוריתמים הבסיסיים המשמשים לניתוח מודל זה פותחו על ידי לאונרד באום, לויד וולש ואנדרו ויטרבי, כשפיתוחים דומים נעשו עוד קודם לכן על ידי המדען הרוסי רוסלן סטרטונוביץ'.

במודל מרקובי פשוט (כמו שרשרת מרקוב) המצב ידוע לצופה ולפיכך הפרמטרים היחידים הם הסתברויות המעבר בין מצבים. במודל מרקוב חבוי לעומת זאת המצב אינו גלוי לצופה בצורה ישירה, אך הפלט, אשר תלוי במצב ידוע לצופה. לכל מצב יש התפלגות של הסתברויות המגדירה את האותיות שאותן הוא יכול לפלוט. רצף אותיות הפלט שאותו מייצר המודל המרקובי החבוי מספק מידע מסוים על רצף המצבים הנסתר.

למודל מרקוב חבוי שימושים בתחומים רבים, בהם למשל זיהוי תבניות בדיבור, כתב יד, חלקי דיבר וביואינפורמטיקה.

הגדרה פורמלית

ניתן להגדיר מודל מרקוב חבוי באופן הבא^[1]:

$\{S_{1},S_{2}...S_{N}\}$ $\{S_{1},S_{2}...S_{N}\}$ - קבוצה של N המצבים במודל.
- נסמן עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ q_t} המצב המתאים לתצפית בזמן t
$\{\sigma _{1},\sigma _{2}...\sigma _{M}\}$ - קבוצה של M אותיות אלפבית (אותיות הפלט של המצבים)
עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle A =\{ a_{ij} \}} - מטריצת הסתברויות מעבר בין מצבים, כאשר $a_{ij}=P[q_{t+1}=S_{j}|q_{t}=S_{i}]$ , כלומר הסתברות מעבר ממצב i למצב j. המטריצה מגדירה הסתברויות ובהתאם צריך להתקיים עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 0 \leq a_{ij} \leq 1} ולכל i מתקיים: עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \sum_j a_{ij}=1}
$B=\{b_{i}(k)\}$ - כאשר עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle b_i(k)} היא ההסתברות לפלט k כאשר נמצאים במצב $S_{i}$ , כלומר עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle b_i(k)=P[v_k at t|q_t=S_i]}
עיבוד הנוסחה נכשל (שגיאת המרה. השרת ("https://en.wikipedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle \Pi =\{\pi _{i}\}} - כאשר עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \pi_i} היא ההסתברות למצב ההתחלתי $S_{i}$

בהיתן מודל עם כל הפרמטרים לעיל, ניתן להשתמש בו כדי ליצור רצף תצפיות: עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ O = o_1 ,..., o_T }

בעיות

באמצעות מודל מרקוב חבוי ניתן לענות על מספר שאלות בנוגע לרצף תצפיות, וכאשר נעשה שימוש בתכנון דינמי ניתן לחשב ביעילות פתרון להן.

הסתברות לרצף תצפיות

בהינתן רצף תצפיות עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle O=o_1,\dots,o_T\,} ובהינתן מודל עם כל פרמטרים לעיל ניתן לחשב את ההסתברות לרצף התצפיות:

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle P(O)=\sum_{X}P(O\mid X)P(X),\,}

כאשר הסכימה נעשית על כל המצבים החבויים האפשריים:

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle X=q_1, \dots, q_T.\,}

אלגוריתם מבוסס תכנון דינמי הפותר בעיה זו הוא אלגוריתם Forward.

הסתברויות למצבים חבויים

בהינתן רצף תצפיות $o_{1},\dots ,o_{T}.$ ובהינתן מודל עם כל פרמטרים לעיל ניתן לחשב את הסתברויות למצבים החבויים ולענות על מספר שאלות.

סינון - המטרה בבעיה זו היא לשערך את ההסתברות של המצב החבוי האחרון, עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle P(q_T\ |\ o_1,\dots,o_T)} . ניתן למצוא פתרון לבעיה באמצעות אלגוריתם Forward.
החלקה - המטרה בבעיה זו היא לשערך את ההסתברות למצב חבוי באמצע הרצף, כלומר $P(q_{k}\ |\ o_{1},\dots ,o_{T})$ , כאשר עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle k < T} . אלגוריתם המבוסס גם כן על תכנון דינמי הפותר בעיה זו הוא אלגוריתם Forward-backward.
פענוח/רצף המצבים הסביר ביותר - בבעיה זו מנסים למצוא מהו רצף המצבים החבויים המסביר בצורה הטובה ביותר את רצף התצפיות לאורך כל הרצף. בעיה זו נפתרת באמצעות אלגוריתם ויטרבי.

למידה

המטרה בבעיה זו היא בהינתן תצפית או אוסף תצפיות לבחור פרמטרים למודל שיתאימו בצורה מיטבית לתיאור התצפיות, כאשר לרוב מחפשים נראות מקסימלית. לא קיים פתרון מדויק לבעיה זו, אך קיים פתרון המאפשר מציאת מקסימום לוקלי של נראות, הידוע כאלגוריתם באום-וולש (Baum–Welch), שהוא מקרה פרטי של אלגוריתם ציפייה - מקסום (Expectation–maximization).

דוגמה

נתאר שני חברים, אליס ובוב, החיים רחוק זה מזו ושמדברים בטלפון מדי יום מה עשו באותו היום. תחומי העניין של בוב הם הליכה בפארק, קניות וניקיון הדירה. הוא בוחר את תעסוקתו היומית אך ורק על פי מזג האוויר באותו היום. לאליס אין מידע על מזג האוויר במקום מגוריו של בוב, אך יש לה מושג כללי, ובהסתמך על המידע שבוב משתף אותה בטלפון היא מנסה לנחש מה מזג האוויר.

אליס מאמינה שמזג האוויר פועל כשרשרת מרקוב, שבה יש שני מצבים "גשום" ו"בהיר". היא לא יודעת במדויק את המצבים מדי יום ולכן זה מידע "חבוי", אך היא יודעת איזו משלוש הפעילויות עשה בוב ("התצפיות").

לאליס יש מושג כללי על מזג האוויר והיא יודעת פחות או יותר מה בוב נוהג לעשות, ועל פי המידע הנ"ל ניתן להגדיר את הפרמטרים של מודל מרקוב חבוי כדלקמן (מתואר בתחביר Python):

מצבים = ('גשום', 'בהיר')
 
תצפיות = ('הליכה', 'קניות', 'ניקיון')
 
הסתברות התחלה = {'גשום': 0.6, 'בהיר': 0.4}
 
הסתברויות מעבר = {
   'גשום' : {'גשום': 0.7, 'בהיר': 0.3},
   'בהיר' : {'גשום': 0.4, 'בהיר': 0.6},
   }
 
הסתברויות פלט= {
   'גשום' : {'הליכה': 0.1, 'קניות': 0.4, 'ניקיון': 0.5},
   'בהיר' : {'הליכה': 0.6, 'קניות': 0.3, 'ניקיון': 0.1},
   }

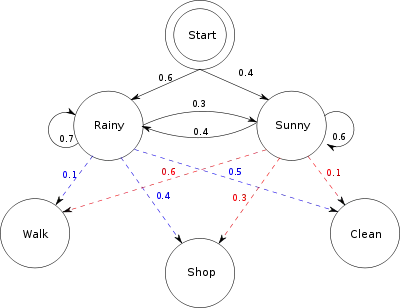
בדוגמה לעיל הסתברויות התחלה (או $\Pi$ ) מייצגים את אמונה של אליס באשר למצב מזג האוויר ביום הראשון שבוב מתקשר אליה (מזג האוויר נוטה יותר לגשום).

הסתברויות מעבר מגדירות את הסתברויות לשינוי מזג האוויר בשרשרת מרקוב. בדוגמה זו, יש סיכוי של 30% בלבד שיום למחרת יום גשום יהיה בהיר. הסתברויות פלט מגדירות את נטייתו של בוב להעדיף פעילות מסוימת בהתאם למצב מזג האוויר. כאשר גשום יש סיכוי של 50% שיעסוק בניקיון; כאשר בהיר, יש סיכוי של 60% שיעשה הליכה בפארק.

תיאור גרפי של מודל מרקוב חבוי בדוגמה

קישורים חיצוניים

ראו מדיה וקבצים בנושא זה בוויקישיתוף.

הערות שוליים

↑ Lawrence R. Rabiner (פברואר 1989). "A tutorial on Hidden Markov Models and selected applications in speech recognition". Proceedings of the IEEE 77 (2): 257–286. doi:10.1109/5.18626.

הערך באדיבות ויקיפדיה העברית, קרדיט,
רישיון cc-by-sa 3.0

This article is issued from Hamichlol. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Lawrence R. Rabiner (פברואר 1989). "A tutorial on Hidden Markov Models and selected applications in speech recognition". Proceedings of the IEEE 77 (2): 257–286. doi:10.1109/5.18626.