נוסחת סטירלינג
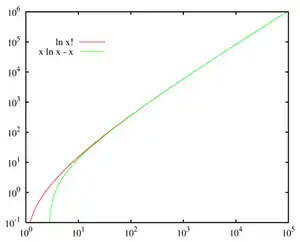
עבור גדול, מתקרב ל־
נוסחת סטירלינג (על-שם המתמטיקאי הסקוטי ג'יימס סטירלינג) היא קירוב מתמטי לערך של (במילים: עצרת) עבור ערכים גדולים של .
זוהי נוסחה אסימפטוטית בשימוש בסימון אסימפטוטי, ופירושה שקיים הגבול
כתוצאה מכך .
בגרסה כללית יותר, הנוסחה נותנת הערכה לפונקציית גמא המהווה הרחבה של פונקציית העצרת.
משפט: קיימת פונקציה ממשית המקיימת עבור -ים גדולים ולכן . כפל של שני האגפים ב- ייתן את הנוסחה ל- .
פיתוח הנוסחה מתבסס על פיתוח אסימפטוטי לטור של האינטגרל המגדיר את פונקציית גמא והפיכתו לאינטגרל של גאוסיאן כפול תיקונים מסדרים שונים.

הערך באדיבות ויקיפדיה העברית, קרדיט,
רישיון cc-by-sa 3.0
רישיון cc-by-sa 3.0
This article is issued from Hamichlol. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.