אינטגרל
אִינְטֶגְרַל הוא מושג מתמטי בתחום החשבון האינפיניטסימלי, המהווה (עבור פונקציה ממשית) הכללה מתמטית של מושג הסכום. את האינטגרל מסמנים בסימן ∫ שניתן על ידי גוטפריד וילהלם לייבניץ ושמקורו ב־s הארוכה שבתחילת המילה הלטינית summa (סכום), שאותה הוא כתב כ-ſumma. האקדמיה ללשון העברית קבעה לו את המונח "אַסְכֶּמֶת" (מלשון "סכום" או "סכימה"), שלא התקבע.
לאינטגרל שימושים רבים ביותר, ובהם חישוב שטח של תחום מישורי, נפח של מרחב רב־ממדי, מסה של גוף, אורך של מסילה עקומה, הסתברות של משתנים מקריים רציפים, כוח הפועל בין שני גופים, אנרגיית החום הכוללת של אמבט, מהירות מקומו המרחבי של גוף הנע בהשפעת כוח בעל עצמה משתנה ועוד.
המושג הכללי של אינטגרל כולל בתוכו שני מושגים שונים לכאורה: האינטגרל המסוים והפונקציה הקדומה (או האינטגרל הלא־מסוים).
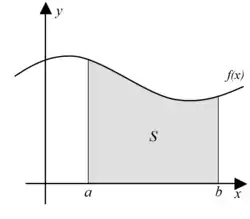
- האינטגרל המסוים של פונקציה אי־שלילית המוגדרת על קטע סופי, הוא מספר השווה לשטח הכלוא בין ציר X לבין גרף הפונקציה, בין קצות הקטע (ראו תרשים משמאל).
- הפונקציה הקדומה או האינטגרל הלא־מסוים של פונקציה מציינים את קבוצת כל הפונקציות הממשיות, שנגזרתן שווה ל־.
המשפט היסודי של החשבון הדיפרנציאלי והאינטגרלי קובע ששני המושגים הללו מתלכדים. כלומר: אם הפונקציה אינטגרבילית בקטע עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle [a,b]} (בהמשך יוגדרו התנאים לאינטגרביליות) וגם יש לה פונקציה קדומה, אז האינטגרל המסוים של בקטע עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle [a,b]} שווה לביטוי , כאשר הפונקציה הקדומה של .
 בערך זה |
האינטגרל המסוים
כאמור לעיל, האינטגרל המסוים של פונקציה ממשית, מעל קטע סגור, שווה לשטח שמתחת לגרף הפונקציה ומעל ציר X (כאשר השטח תחת ציר X מוגדר כשטח שלילי). כדי לקבל הגדרה מסודרת של האינטגרל, יש לבחון את המשמעות המדויקת של המושג "שטח", במיוחד כאשר הגרף אינו ישר, ואף אינו בהכרח רציף. השטח של מלבן מובן היטב, ואחת הדרכים להגדיר את השטח שמתחת לגרף היא לקרב את הצורה שמתחת לגרף באמצעות מלבנים זרים (ומקבילים לצירים). בהגדרה זו יש בעיה עקרונית: כל עוד מספר המלבנים סופי, והפונקציה אינה מלבנית, השטח הכולל שלהם אינו אלא קירוב של השטח האמיתי, וניתן לשפר את הקירוב על ידי הקטנת המלבנים והגדלת מספרם.
ברנהרד רימן הפך את הבעיה הזו להגדרה של ערך האינטגרל: במקום לחפש את הקירוב הטוב ביותר, שלרוב אינו קיים, מסכמים מלבנים קטנים ורבים יותר, כך שהקירוב ילך וישתפר. בסופו של דבר בוחרים את הגבול של סדרת הסכומים המתקבלת מסדרת הקירובים. גישה דומה, המגיעה לאותן תוצאות, מבוססת על סכומי דארבו: כאן מקרבים את הצורה החוסמת מלמטה ומלמעלה באמצעות מלבנים הכלואים מתחת לגרף ומלבנים הכולאים אותו מלמעלה.
הראשון שהגדיר את האינטגרל המסוים במדויק היה רימן. בעקבותיו הוצעו הכללות רבות: בתחום ההגדרה של הפונקציה (העשוי להיות הישר הממשי כולו, קובייה במרחב האוקלידי ה־־ממדי, או כל מרחב קומפקטי מקומית), בערכים שהפונקציה עשויה לקבל (מספרים ממשיים או מרוכבים, מספרים p־אדיים, או וקטורים שאלו רכיביהם), ובאופי הפונקציות שעבורן מחושב האינטגרל.
חלוקה של קטע
סדרה (סופית) של נקודות עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a=x_0<x_1<\cdots<x_{n-1}<x_n=b} נקראת חלוקה של הקטע עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle [a,b]} .
את הסדרה אפשר לפרש כאילו היא שוברת את הקטע ל־ "תת־קטעים" עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle [x_0,x_1],[x_1,x_2],\ldots,[x_{n-1},x_n]} , החותכים זה את זה רק בנקודות הקצה שלהם. לכל חלוקה אפשר להגדיר את קוטר החלוקה (או פרמטר החלוקה) – עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \lambda(P)=\max_{1\le i\le n}|x_i-x_{i-1}|} . מכיוון שסכום אורכי הקטעים הוא עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle b-a} , הקוטר של חלוקה בת קטעים הוא לפחות עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \frac{b-a}{n}} . מכאן שכדי לקרב את קוטר החלוקה לאפס, יש להגדיל את מספר הנקודות באופן שאינו חסום.
חלוקה היא עידון של חלוקה , אם החלוקה הראשונה כוללת את כל הנקודות המופיעות בחלוקה השניה. למשל, עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a=x_0<x_1<x_2<x_3=b} מעדנת את עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a=x_0<x_2<x_3=b} . ברור שבמקרה כזה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \lambda(P')\le\lambda(P)} .
הגדרת האינטגרל המסוים באמצעות סכומי רימן
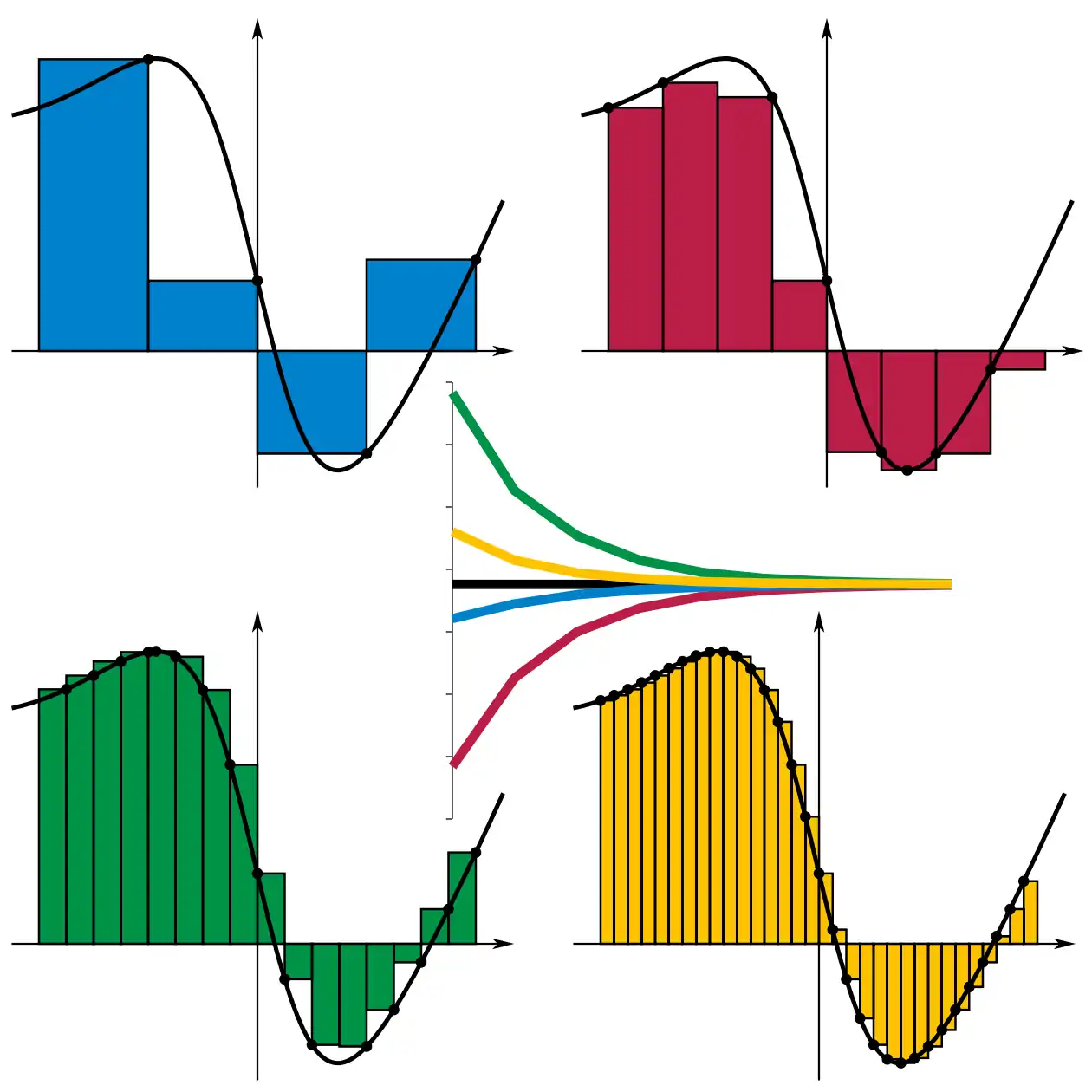
כחול – חלוקה בה בוחרים בכל תת-קטע את הנקודה הימנית
כתום – הנקודה השמאלית
ירוק – נקודת המקסימום בתת-הקטע
אדום – נקודת המינימום
הגרף שבמרכז מתאר את התנהגות ארבעת הקירובים כאשר מספר המלבנים גדל. מכיוון שהפונקציה אינטגרבילית, כל הקירובים שואפים לאותו ערך
בחלוקה נתונה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a=x_0<x_1<\cdots<x_{n-1}<x_n=b} , אפשר לבחור נקודה מכל תת־קטע. חלוקה כזו, יחד עם הנקודות שנבחרו מתת־הקטעים, נקראת חלוקה מסומנת. לחלוקה כזו אפשר להגדיר את סכום רימן
זהו השטח הכולל של המלבנים שבסיסם הוא הקטע וגובהם (עבור ), כאשר השטח הוא "שטח מכוון" (העשוי להיות חיובי או שלילי, בהתאם לסימן של הפונקציה בנקודה ). כל סכום רימן מהווה קירוב לשטח שמתחת לגרף הפונקציה, בקטע המדובר עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle [a,b]} .
פונקציה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f(x)} המוגדרת בקטע עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle [a,b]} , היא אינטגרבילית לפי רימן, אם לכל בחירה של סדרת חלוקות עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle P_1,P_2,\ldots} בעלות גדלים השואפים לאפס, הגבול עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \lim_{m\to\infty}\sigma(f,P_m)} קיים (היינו, הסדרה מתכנסת).
במקרה כזה, כל הגבולות עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \lim_{m\to\infty}\sigma(f,P_m)} שווים זה לזה[1], וגבולן המשותף הוא, כעניין שבהגדרה, ערכו של האינטגרל המסוים. אם הגבולות האלה אינם קיימים, הפונקציה אינה "אינטגרבילית", ואז אין לאינטגרל המסוים כל מובן מספרי. מאידך, כאשר הפונקציה אינטגרבילית, השטח שמתחת לגרף הוא ערכו של האינטגרל.
את ערך האינטגרל מסמנים כך: . המשתנה בביטוי זה הוא "משתנה האינטגרציה", ולשמו אין כל חשיבות: אפשר לכתוב באותה מידה או . הביטוי שבתוך האינטגרל נקרא אינטגרנד.
הגדרה באמצעות סכומי דארבו
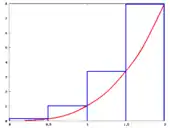
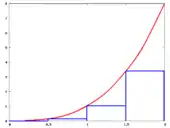
נניח כי חסומה בקטע סגור עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle [a,b]} . לכל חלוקה , אפשר לחשב בנפרד את השטח שהחלוקה מאתרת מתחת לגרף, ואת השטח שהחלוקה מאתרת מעל לגרף.
לצורך כך נסמן בכל תת־קטע של החלוקה, את החסם העליון של הפונקציה , ואת החסם התחתון עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle m_i} (אם לפונקציה יש בתת-הקטע הזה ערך מינימלי או מקסימלי, אלו יהיו ערכי עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle m_i,M_i} בהתאמה). באופן הזה, מובטח כי לכל בתת־הקטע.
משום כך סביר לקבוע ששטחו של התחום המישורי המוגבל על ידי ציר X, גרף הפונקציה, והישרים , גדול או שווה לשטח המלבן עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle m_i|x_i-x_{i-1}|} , וקטן (או שווה) לשטח המלבן .
אם נסכם את כל המלבנים, הסכום עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \underline S(P)=\sum_{i=1}^n m_i|x_i-x_{i-1}|} נקרא הסכום התחתון של החלוקה, ואילו הוא הסכום העליון שלה.
קל להוכיח שאם מהווה עידון של , אזי עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \underline S(P)\le\underline S(P')\le\bar S(P')\le\bar S(P)} , ולכן כאשר מעדנים את החלוקה, המרחק בין הסכום העליון לתחתון מצטמצם.
החסם התחתון של כל הסכומים העליונים עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \bar S(P)} , עבור כל החלוקות האפשריות, הוא האינטגרל העליון. החסם העליון של כל הסכומים התחתונים עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \underline S(P)} הוא האינטגרל התחתון.
הפונקציה אינטגרבילית לפי דארבו, אם שני ערכים אלו שווים זה לזה – פירוש השוויון הוא שקיימת סדרת חלוקות המעדנות זו את זו, כך שההפרש .
אפשר להוכיח שהגדרת אינטגרביליות של פונקציה חסומה באמצעות סכומי רימן שקולה להגדרה באמצעות סכומי דארבו, ושהאינטגרל המתקבל בשני המקרים שווה.
ההגדרה שנתנה לעיל מתאימה לפונקציות חסומות, ולחישוב מעל קטע סגור. עם זאת, אפשר להרחיב את ההגדרה גם למקרים כלליים יותר – ראו אינטגרל לא אמיתי.
מרחב הפונקציות האינטגרביליות
הסכום של פונקציות אינטגרביליות (לפי רימן) והכפולה של פונקציה אינטגרבילית בסקלר נותנים פונקציות אינטגרביליות; לכן אוסף הפונקציות האינטגרביליות מעל קטע קבוע עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle [a,b]} מהווה מרחב וקטורי מעל שדה המספרים הממשיים.
משפט לבג מאפיין אינטגרביליות באופן הבא: פונקציה חסומה היא אינטגרבילית במובן רימן, אם ורק אם קבוצת נקודות אי־הרציפות שלה היא בעלת מידה אפס.
למשל, כל פונקציה רציפה וכל פונקציה מונוטונית בקטע סגור, היא אינטגרבילית. גם פונקציית רימן אינטגרבילית (והאינטגרל שלה הוא אפס). לעומת זאת, פונקציית דיריכלה אינה אינטגרבילית לפי רימן.
ההתאמה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f\mapsto\int\limits_a^b f(x)dx} היא פונקציונל לינארי המוגדר על המרחב הזה, משום שהאינטגרל של פונקציות מקיים את התכונה .
האינטגרל מונוטוני, במובן הבא: אם עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f,g} אינטגרביליות בקטע עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle [a,b]} , ולכל מתקיים עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f(x)\ge g(x)} , אז ואם עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f(x)>g(x)} לכל אז מתקיים אי־השוויון החזק .
חישוב האינטגרל המסוים
נוסחת ניוטון-לייבניץ מחשבת את האינטגרל המסוים, אם ידוע האינטגרל הלא־מסוים (ראו להלן). במקרים אחרים יש להפעיל שיטות אנליטיות מיוחדות, או שיטות נומריות.
האינטגרל הלא־מסוים
הגדרה
פונקציה נקראת פונקציה קדומה של עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f(x)} בקטע כלשהו, אם לכל נקודה בקטע . כלומר עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f(x)} היא הנגזרת של בקטע.
האינטגרל הלא-מסוים של פונקציה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f(x)} מוגדר לרוב בתור אוסף הפונקציות הקדומות שלו. בסימון: , כאשר היא פונקציה קדומה של עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f(x)} ו- הוא קבוע שרירותי.
ניתן להצדיק את הסימון בכך שכל הפונקציות הקדומות של פונקציה ניתנות לכתיבה בתור קבוע ועוד פונקציה קדומה כלשהי.
מצד אחד, אם אז ברור כי גם כי נגזרת של קבוע היא 0.
מצד שני, אם עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle F(x),G(x)} פונקציות קדומות של עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f(x)} אז מתקיים , כלומר הפונקציה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle F(x)-G(x)} קבועה, כלומר עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle F(x)-G(x)=C} , כנדרש.
בהינתן פונקציה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f(x)} אינטגרבילית בקטע הסגור עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle [a,b]} ניתן להגדיר פונקציה באופן הבא:
ערכה של פונקציה זו בכל נקודה הוא ערך האינטגרל המסוים של עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f(x)} בין נקודה זו לנקודת מוצא כלשהי. פונקציה זו היא תמיד רציפה, אך אינה בהכרח גזירה ולכן אינה בהכרח פונקציה קדומה של עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f(x)} . עבור פונקציית מדרגה, למשל, לא יהיה אינטגרל זה גזיר, שכן פונקציית מדרגה אינה מקיימת את תכונת הנגזרת הבאה לידי ביטוי במשפט דארבו.
המשפט היסודי של החשבון הדיפרנציאלי והאינטגרלי אומר כי גזירה בכל מקום בו עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f(x)} רציפה. כלומר: אם עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f(x)} רציפה ב- אזי מתקיים . כלומר, היא פונקציה קדומה של עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f(x)} באופן כללי, לא חייבת להיות גזירה בכל מקום.
על כן, המשפט היסודי קושר בין האינטגרל המסוים ובין האינטגרל הלא מסוים של הפונקציה, וממנו נגזרת הנוסחה היסודית המאפשרת לחשב אינטגרל מסוים באמצעות שימוש בפונקציה קדומה.
דוגמה
ידוע כי הנגזרת של עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle x^2} היא עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 2x} . על כן כל פונקציה קדומה של עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 2x} נבדלת מ-עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle x^2} בקבוע, ונכתוב:
מציאת האינטגרל הלא-מסוים
בניגוד לפעולת הגזירה, שהיא טכנית בעיקרה ומבוססת על כמה כללים ברורים היטב, אין "מתכון" בטוח למציאת אינטגרל לא מסוים של פונקציה.
באמצעות נוסחאות הגזירה ניתן למצוא מיידית אינטגרלים לפונקציות האלמנטריות הבסיסיות, ועל מנת לבצע אינטגרציה לפונקציות מסובכות יותר ישנן שיטות אינטגרציה (החלפת משתנים, אינטגרציה בחלקים ועוד) שמאפשרות לפשט את הפונקציה ולהפוך אותה לפונקציה אחרת, שעבורה קל יותר למצוא את האינטגרל.
גם אם לא ניתן לבטא את האינטגרל הלא-מסוים באמצעות פונקציה אנליטית, אין זה אומר שהאינטגרל המסוים אינו קיים. בהרבה מקרים (למשל במשוואות דיפרנציאליות) ביטויים מהצורה נחשבים לפתרון קביל.
הערות
למעשה, סכום רימן הוא חלוקה של הקטע למלבנים צרים שגובהם הוא , סיכום שטחיהם ומעבר לגבול כאשר פרמטר החלוקה שואף לאפס. באנליזה נומרית יש חשיבות גדולה לבחירת נקודות הביניים כדי לקבל התכנסות מהירה של הקירוב הנומרי לערך המדויק (שלרוב אינו ניתן לחישוב).
הכללות של אינטגרל רימן
אינטגרל לבג

אינטגרל לבג הוא הכללה של אינטגרל רימן לפונקציות מדידות שפותחה על ידי המתמטיקאי אנרי לבג במסגרת מחקרו על תורת המידה. אינטגרל לבג מתבסס על מידת לבג המוגדרת מעל הישר הממשי והוא מזדהה עם אינטגרל רימן לכל פונקציה חסומה שהיא אינטגרבילית במובן רימן.
בהיות האינטגרל של לבג הכללה של אינטגרל רימן, מאפשר מושג זה לחשב אינטגרל לפונקציות שאינן אינטגרביליות רימן. הרעיון באינטגרל לבג הוא לחשב את השטח לפי התמונה של הפונקציה ולא לפי התחום שלה. היתרון בגישה זו היא שלרוב התמונה של הפונקציה פשוטה בהרבה ו"פתולוגית" הרבה פחות מתחום הגדרתה. לכן, מחלקת הפונקציות שהן אינטגרביליות במובן לבג רחבה יותר ממחלקת הפונקציות האינטגרביליות רימן. למעשה, גם פונקציות שאינן רציפות באף מקום יכולות להיות אינטגרביליות לבג (בעוד שאינן אינטגרביליות רימן). אחת הדוגמאות הבסיסיות והיפות לפונקציה כזאת היא פונקציית דיריכלה.
אינטגרל רימן־סטילטיס ואינטגרל לבג־סטילטיס
אינטגרל רימן-סטילטיס הוא הכללה אחרת של אינטגרל רימן.
אינטגרל רימן־סטילטיס של פונקציה ממשית של משתנה ממשי ביחס לפונקציה ממשית מסומן:
ומוגדר להיות הגבול של הביטוי:
כאשר נמצא ברווח ה־ בחלוקת הקטע עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle [a,b]} לקטעים וכאשר אורך הקטע המקסימלי בחלוקה שואף ל־0.
האינטגרל אינו מוגדר כאשר לשתי הפונקציות עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f,g} יש נקודת אי־רציפות משותפת. יש הכללה שתגדיר את האינטגרל כאשר בנקודת אי-הרציפות המשותפת אחת הפונקציות רציפה מימין והשנייה משמאל.
הכללה נוספת היא אינטגרל לבג-סטילטיס, שהוא הכללה הן של אינטגרל רימן־סטילטיס והן של אינטגרל לבג. שתי ההגדרות, של אינטגרל רימן־סטילטיס ושל אינטגרל לבג־סטילטיס הן הגדרות זהות כאשר הפונקציה היא פונקציה מונוטונית עולה, וזהו המקרה בו אינטגרל זה משמש בסטטיסטיקה ובמשתנים מקריים כאשר הפונקציה היא פונקציה ההסתברות (המצטברת).
שימושי האינטגרל
שימוש חשוב של האינטגרל הוא מציאת שטח. השטח בין פונקציה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f(x)} אי־שלילית (כלומר: עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \forall x:f(x)\ge0} ) בקטע עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle [a,b]} ובין ציר הוא עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \int\limits_a^b f(x)dx} .
כאשר עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f(x)} מקבלת גם ערכים שליליים, האינטגרל מחשב את השטח הכלוא בין גרף הפונקציה לציר אך מחזיר אותו עם סימן בהתאם למיקום של השטח ביחס לציר :
סימן חיובי אם השטח כלוא מעל ציר וסימן שלילי אם השטח כלוא מתחתיו. למשל: עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \int\limits_{-1}^0x\,dx=-\tfrac12} .
כך ייתכן למשל, ששטחים יקזזו זה את זה כאשר חלק מהם מעל לציר וחלק מהם מתחתיו. למשל: עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \int\limits_{-1}^1x\,dx=0} בעוד ש-
- אורך גרף הפונקציה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f(x)} הגזירה ברציפות בקטע עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle [a,b]} הוא .
- זאת כמקרה פרטי של הנוסחה לאורך עקומה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \gamma(t)} גזירה ברציפות ורגולרית:
בנוסף, אפשר להשתמש באינטגרל לחישוב נפח גוף סיבוב. גוף סיבוב הוא גוף המתקבל על ידי סיבוב פונקציה סביב ציר .
- נפח גוף הסיבוב של הפונקציה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f(x)} בקטע עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle [a,b]} הוא .
- נפח גוף הסיבוב המתקבל בין הפונקציות הוא .
- נפח גוף סיבוב סביב ציר של עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f(x)} בקטע עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle [a,b]} הוא .
- שטח הפנים של גוף סיבוב הוא (ללא שטח הבסיסים) .
- נפח גוף ששטח החתך שלו לכל הוא עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle A(x)} שווה .
- הערך הממוצע של ערכי הפונקציה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f(x)} בקטע עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle [a,b]} הוא עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \begin{align}\frac1{b-a}\int\limits_a^b f(x)dx\end{align}} .
|
עיינו גם בפורטל
פורטל המתמטיקה הוא שער לכל הנושאים הקשורים במתמטיקה. ניתן למצוא בו קישורים אל תחומי המשנה של ענף המתמטיקה, מושגי יסוד בתחום, היסטוריה של המתמטיקה, מתמטיקאים חשובים ועוד. |
ראו גם
קישורים חיצוניים
- מחשבון אינטגרלים בעברית
- מחשבון אינטגרלים
- מחשבון אינטגרל רימן-סטילטיס
- גדי אלכסנדרוביץ', אז מה זה אינטגרל?, באתר "לא מדויק"
- אינטגרל, באתר MathWorld (באנגלית)
הערות שוליים
- ↑ אכן, אם הגבולות לארכן של שתי סדרות שונים זה מזה, אז לסדרת הסכומים המתקבלים משילוב הסדרות של חלוקות לסירוגין, פעם זו ופעם זו, לא יהיה גבול

רישיון cc-by-sa 3.0
