פונקציית האינטגרל הלוגריתמי

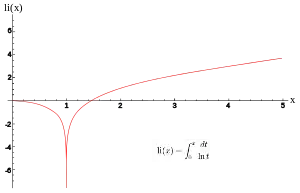
גרף של פונקציית האינטגרל הלוגריתמי

במתמטיקה, פונקציית האינטגרל הלוגריתמי היא פונקציה מתמטית חשובה, הידועה בעיקר בזכות משפט המספרים הראשוניים. היא מוגדרת להיות:

{\text{li}}(x)=\int \limits _{0}^{x}{\frac {dt}{\ln(t)}}

לפונקציה ${\tfrac {1}{\ln(t)}}$ יש סינגולריות בתחום $t=1$ , אז הפונקציה מוגדרת במפורש לכל $x<1$ , ומוגדרת לכל $x>1$ על ידי עקרון הערך של קושי, על ידי:

{\text{li}}(x)=\lim _{\varepsilon \to 0^{+}}\left(\int \limits _{0}^{1-\varepsilon }{\frac {dt}{\ln(t)}}+\int \limits _{1+\varepsilon }^{x}{\frac {dt}{\ln(t)}}\right)

פונקציית האינטגרל הלוגריתמי ההפוך

פונקציית האינטרגל הלוגריתמי או פונקציית האינטגרל הלוגריתמי של אוילר מוגדרת להיות:

{\text{Li}}(x)={\text{li}}(x)-{\text{li}}(2)

או בצורה אינטגרלית:

{\text{li}}(x)=\int \limits _{2}^{x}{\frac {dt}{\ln(t)}}

פונקציה זו אינה בעלת נקודה סינגולרית. פונקציה זו יותר מדויקת בחישוב כמות של מספרים ראשונים הקטנים מ- $x$ .

הצגות נוספות של פונקציית האינטגרל הלוגריתמי

הצגה על ידי פונקציית האינטגרל האקספוננטי

לפונקציה יש קשר עם פונקציית האינטגרל האקספוננטי על ידי המשוואה:

{\text{li}}(x)={\text{Ei}}{\bigl (}\ln(x){\bigr )}

שנפתרת על ידי כל מספר חיובי. קשר נוסף הוא על ידי קבוע אוילר-מסקרוני:

{\text{li}}(e^{u})={\text{Ei}}(u)=\gamma +\ln {\bigl (}|u|{\bigr )}+\sum _{n=1}^{\infty }{\frac {u^{n}}{n\cdot n!}}\quad :u\neq 0

חישוב נוסף של פונקציית האינטגרל הלוגריתמי היא:

{\text{li}}(x)=\gamma +\ln {\bigl (}\ln(x){\bigr )}+{\sqrt {x}}\sum _{n=1}^{\infty }\left(-{\tfrac {1}{2}}\right)^{n-1}{\frac {\ln(x)^{n}}{n!}}\sum _{k=0}^{\left\lfloor {\frac {n-1}{2}}\right\rfloor }{\frac {1}{2k+1}}

הצגה על ידי הרחבה אסימפטוטית

ניתן להציג את פונקציית האינטגרל הלוגריתמי גם על ידי הרחבה אסימפטוטית שיש לו. למשל:

{\text{li}}(x)=O\left({\frac {x}{\ln(x)}}\right)

כאשר O מייצג את סימן O גדולה. רישום מלא של הפונקציה על ידי הרחבה אסימפטוטית הוא:

{\text{li}}(x)\sim {\frac {x}{\ln(x)}}\sum _{k=0}^{\infty }{\frac {k!}{\ln(x)^{k}}}

או:

{\frac {{\text{li}}(x)}{\frac {x}{\ln(x)}}}\sim 1+{\frac {1}{\ln(x)}}+{\frac {2}{\ln(x)^{2}}}+{\frac {6}{\ln(x)^{3}}}+\cdots

רישום זה גורר לרישום הבא:

{\text{li}}(x)-{\frac {x}{\ln(x)}}=O\left({\frac {x}{\ln(x)^{2}}}\right)

הערה, הרישום האחרון כסדרה אינו מתכנס, אז חשוב לסדרה תהיה מספר סופי של אברים.

ערכים מיוחדים של הפונקציה

לפונקציה יש שורש חיובי יחיד, הידוע בתור קבוע רמנוג'אן-סולדר, אשר קרוב שלה הוא $x\approx 1.4513692348\ldots$ . בנוסף לכך, ערך הפונקציה בנקודה $x=2$ הוא גם $-{\bigl (}\Gamma {\bigl (}0,-\ln(2){\bigr )}+\pi i{\bigr )}$ כאשר $\Gamma (a,x)$ היא פונקציית גמא הלא-שלמה.

ראו גם

This article is issued from Hamichlol. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.