קבוע אוילר-מסקרוני

השטח הכחול הכלוא בין גרף ${\displaystyle {\tfrac {1}{\lfloor x\rfloor }}}$ לגרף עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \tfrac1x} בקטע מ-1 עד אינסוף שווה לקבוע אוילר-מסקרוני

בערך זה נעשה שימוש בסימנים מוסכמים מתחום המתמטיקה. להבהרת הסימנים ראו סימון מתמטי.

קבוע אוילר (גם קבוע אוילר-מסקרוני או קבוע מסקרוני) הוא קבוע מתמטי, שהשימוש העיקרי שלו הוא בתורת המספרים, המסומן באות גמא (${\displaystyle \gamma }$) ומוגדר על ידי הגבול:

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \gamma=\lim_{n\to\infty}\left[\sum_{k=1}^n\frac1k-\ln(n)\right]=\lim_{n\to\infty}\left[1+\cdots+\frac1n-\ln(n)\right]=0.577215664901532860\ldots}

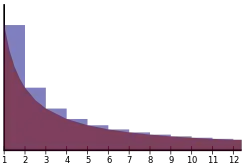
כלומר קבוע אוילר הוא ההפרש האסימפטוטי בין הטור ההרמוני ללוגריתם הטבעי.

הפרש זה מתכנס באופן טבעי משום שמתקיים עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ln(n)=\int\limits_1^n\frac1x\,dx} ולכן הסכום ${\displaystyle \sum _{k=1}^{n}{\frac {1}{k}}}$ הוא מן "גרסה בדידה" של הלוגריתם הטבעי.

מכאן נובעת דרך תיאור נוספת של הקבוע:

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \begin{align}\int\limits_1^\infty\left(\frac1{\lfloor x\rfloor}-\frac1x\right)dx\end{align}}

כאשר עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \lfloor x\rfloor} הוא הערך השלם התחתון של עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle x} .

לא ידוע אם קבוע אוילר רציונלי או אי-רציונלי.

היסטוריה

הקבוע הוגדר לראשונה על ידי המתמטיקאי השווייצרי לאונרד אוילר במאמרו "De Progressionibus harmonicus observationes" אשר פורסם בשנת 1735. אוילר השתמש בסימון C עבור הקבוע, וחישב בראשונה את ערכו בדיוק של 6 ספרות אחרי הנקודה. בשנת 1761 הוא הרחיב את החישוב, ופרסם אותו בדיוק של 16 ספרות אחרי הנקודה.

בשנת 1790 הציע המתמטיקאי האיטלקי לורנצו מסקרוני את סימון הקבוע באות ${\displaystyle \gamma }$ (גמא היוונית), וניסה להרחיב את ערכו של הקבוע עד ל-32 ספרות אחרי הנקודה, אם כי חישובים מאוחרים יותר גילו כי מסקרוני שגה בחישוב הספרה ה-20 אחרי הנקודה. המתמטיקאי ההודי סריניוואסה רמנוג'אן מצא טורים שונים המתכנסים ל-${\displaystyle \gamma }$ .

כפי שנאמר, לא ידוע האם קבוע אוילר הוא מספר רציונלי או לא. עם זאת, ניתוח שבר משולב מראה כי אם קבוע אוילר הוא רציונלי, הרי שהמכנה בשבר המגדיר אותו לא יהיה קטן מ-${\displaystyle 10^{242080}}$ .

תכונות

ניתן לקבל את ערכו של הקבוע גם על פי האינטגרלים הבאים:

${\displaystyle {\begin{aligned}\gamma &=-\int \limits _{0}^{\infty }e^{-x}\ln(x)\,dx\\&=-\int \limits _{0}^{1}\ln \!\left(\ln \left({\frac {1}{x}}\right)\right)dx\\&=\int \limits _{0}^{\infty }\left({\frac {1}{1-e^{-x}}}-{\frac {1}{x}}\right)e^{-x}\,dx\\&=\int \limits _{0}^{\infty }{\frac {1}{x}}\left({\frac {1}{1+x}}-e^{-x}\right)dx\end{aligned}}}$

אינטגרלים אחרים אשר מכילים את ערך ${\displaystyle \gamma }$ הם:

${\displaystyle {\begin{aligned}\int \limits _{0}^{\infty }e^{-x^{2}}\ln(x)dx=-{\frac {\sqrt {\pi }}{4}}{\big (}\gamma +2\ln(2){\big )}\end{aligned}}}$

${\displaystyle {\begin{aligned}\int \limits _{0}^{\infty }e^{-x}\ln(x)^{2}dx=\gamma ^{2}+{\frac {\pi ^{2}}{6}}\end{aligned}}}$

ניתן לבטא את קבוע אוילר גם בעזרת אינטגרל כפול:

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \begin{align}\gamma=\int\limits_0^1\int\limits_0^1\frac{x-1}{(1-xy)\ln(xy)}\,dx\,dy\end{align}}

בדומה האינטגרל הכפול הבא שהוצג על ידי ג'. סונדאו (2005):

${\displaystyle {\begin{aligned}\ln \left({\frac {4}{\pi }}\right)=\int \limits _{0}^{1}\int \limits _{0}^{1}{\frac {x-1}{(1+xy)\ln(xy)}}\,dx\,dy\end{aligned}}}$

מראה כי ניתן להסתכל על ${\displaystyle \ln \left({\frac {4}{\pi }}\right)}$ בתור "קבוע אוילר חילופי".

בשנת 1910, הציג ואקה את הסכום הבא:

${\displaystyle {\begin{aligned}\gamma =\sum _{n=1}^{\infty }(-1)^{n}{\frac {{\bigl \lfloor }\log _{2}(n){\bigr \rfloor }}{n}}\end{aligned}}}$

כאשר ${\displaystyle \log _{2}}$ הלוגריתם בבסיס 2 ו-${\displaystyle \lfloor \,\rfloor }$ פונקציית הערך השלם.

ניתן לקבל את סדרתו של ואקה על ידי מניפולציה של אינטגרל Catalan.

${\displaystyle {\begin{aligned}\gamma =\int \limits _{0}^{1}{\frac {1}{1+x}}\sum _{n=1}^{\infty }x^{2^{n}-1}\,dx\end{aligned}}}$

קשרים לפונקציות מיוחדות

ניתן לבטא את קבוע אוילר גם כטור אינסופי של איברים הכוללים ערכים של פונקציית זטא של רימן של מספרים שלמים וחיוביים:

${\displaystyle {\begin{aligned}\gamma &=\sum _{m=2}^{\infty }{\frac {(-1)^{m}\zeta (m)}{m}}\\&=\ln \left({\frac {4}{\pi }}\right)+\sum _{m=1}^{\infty }{\frac {(-1)^{m-1}\zeta (m+1)}{2^{m}(m+1)}}\end{aligned}}}$

סדרות נוספות הקשורות לפונקציית זטא של רימן:

${\displaystyle {\begin{aligned}\gamma &={\frac {3}{2}}-\ln(2)-\sum _{m=2}^{\infty }(-1)^{m}{\frac {m-1}{m}}{\bigl [}\zeta (m)-1{\bigr ]}\\&=\lim _{n\to \infty }\left[{\frac {2^{n}}{e^{2^{n}}}}\sum _{m=0}^{\infty }{\frac {2^{mn}}{(m+1)!}}\sum _{t=0}^{m}{\frac {1}{t+1}}-n\ln(2)+O\left({\frac {1}{2^{n}e^{2^{n}}}}\right)\right]\\&=\lim _{n\to \infty }\left[{\frac {2n-1}{2n}}-\ln(n)+\sum _{k=2}^{n}\left({\frac {1}{k}}-{\frac {\zeta (1-k)}{n^{k}}}\right)\right]\end{aligned}}}$

כמו כן, ניתן לבטא את הקבוע על ידי פונקציית בטא (במונחים של פונקציות גמא):

${\displaystyle \gamma =\lim _{n\to \infty }\left[{\frac {\Gamma ({\frac {1}{n}})\Gamma (n+1)n^{1+{\frac {1}{n}}}}{\Gamma \left(2+n+{\frac {1}{n}}\right)}}-{\frac {n^{2}}{n+1}}\right]}$

שני גבולות השווים בערכם לקבוע אוילר-מסקרוני הם הגבול האנטי-סימטרי:

${\displaystyle \gamma =\lim _{s\to 1}\sum _{n=1}^{\infty }\left({\frac {1}{n^{s}}}-{\frac {1}{s^{n}}}\right)}$

והגבול

${\displaystyle \gamma =\lim _{x\to \infty }\left[x-\Gamma \left({\frac {1}{x}}\right)\right]=\lim _{n\to \infty }{\frac {1}{n}}\sum _{k=1}^{n=1}\left(\left\lceil {\frac {n}{k}}\right\rceil -{\frac {n}{k}}\right)}$

סדרת זטא הרציונלית היא ביטוי קשור מאד לנוסחה שהוצגה לעיל. אם נסיר מספר איברים מהסדרה לעיל, ניתן לקבל הערכה לגבול סדרה הקלאסי:

${\displaystyle \gamma =\sum _{k=1}^{n}{\frac {1}{k}}-\ln(n)-\sum _{m=2}^{\infty }{\frac {\zeta (m,n+1)}{m}}}$

כאשר ${\displaystyle \zeta (s,k)_{}^{}}$ היא פונקציית הורביץ-זטא. הסכום במשוואה זה מערב מספרים הרמוניים, המסומנים ${\displaystyle H_{n}}$ . הרחבת מספר איברים בפונקציית הורביץ-זטא מביא אותנו למשוואה:

${\displaystyle H_{n}=\ln(n)+\gamma +{\frac {1}{2n}}-{\frac {1}{12n^{2}}}+{\frac {1}{120n^{4}}}-\varepsilon }$

כאשר ${\displaystyle 0<\varepsilon <{\frac {1}{252n^{6}}}}$

לבסוף, ניתן לחשב את הקבוע כנגזרת של פונקציית גמא של אוילר:

${\displaystyle \gamma =-\Gamma '(1)}$

e^γ

הקבוע ${\displaystyle e^{\gamma }}$ נחשב גם הוא לקבוע חשוב בתורת המספרים. מדי פעם, מסמנים קבוע זה גם ${\displaystyle \gamma '}$ ומבטאים אותו בעזרת הגבול הבא, כאשר ${\displaystyle p_{n}}$ הוא המספר הראשוני ה-${\displaystyle n}$-י:

${\displaystyle e^{\gamma }=\lim _{n\to \infty }{\frac {1}{\ln(p_{n})}}\prod _{i=1}^{n}{\frac {p_{i}}{p_{i}-1}}}$

אשר מהווה ניסוח מחודש לשלישי מבין משפטי מרטן. הערך המספרי של ${\displaystyle e^{\gamma }}$ הוא:

${\displaystyle e^{\gamma }=1.78107241799019798523650410310717954916964521430343\ldots }$

מכפלות אינסופיות נוספות הקשורות לערך של קבוע זה הן:

${\displaystyle {\begin{aligned}{\frac {e^{1+{\frac {\gamma }{2}}}}{\sqrt {2\pi }}}&=\prod _{n=1}^{\infty }e^{-1+{\frac {1}{(2n)}}}\left(1+{\frac {1}{n}}\right)^{n}\\{\frac {e^{3+2\gamma }}{2\pi }}&=\prod _{n=1}^{\infty }e^{-2+{\frac {2}{n}}}\left(1+{\frac {2}{n}}\right)^{n}\end{aligned}}}$

שתי המכפלות הללו נובעות פונקציית ${\displaystyle G}$ של בארנס. כמו כן:

${\displaystyle e^{\gamma }=\left({\frac {2}{1}}\right)^{\frac {1}{2}}\left({\frac {2^{2}}{1\cdot 3}}\right)^{\frac {1}{3}}\left({\frac {2^{3}\cdot 4}{1\cdot 3^{3}}}\right)^{\frac {1}{4}}\cdots }$

שהוצג על ידי ג'ונתן סונדאו על ידי שימוש בפונקציות היפר-גאומטריות.

מופעים

קבוע אוילר-מסקרוני מופיע, בנוסף למקומות אחרים, גם ב:

• אי-שוויון עבור פונקציית אוילר.
• שיעור צמיחה של פונקציית המחלקים.
• נוסחת כפל עבור פונקציית גמא.
• חישוב של פונקציית דיגאמה.
• ביטויים הכוללים את האינטגרל המעריכי.
• האיבר הראשון בפיתוח טור טיילור עבור פונקציית זטא של רימן.

ראו גם

• טור ההופכיים של המספרים הראשוניים

לקריאה נוספת

קישורים חיצוניים

• קבוע אוילר-מסקרוני, באתר MathWorld (באנגלית)