פונקציית הזהות

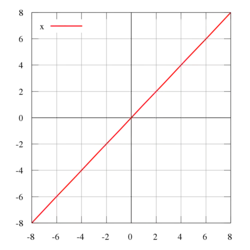
הגרף של פונקציית הזהות על מערכת צירים

פונקציית הזהות או טרנספורמציית הזהות היא פונקציה שמחזירה תמיד את אותו הערך שעליו היא פעלה, פונקציה f היא פונקציית הזהות אם לכל איבר x בקבוצה M עליה היא פועלת מתקיים f(x) = x.

פונקציית הזהות על קבוצה M מסומנת לעיתים על ידי id_M או 1_M.

תכונות אלגבריות

תהי f : M → N פונקציה כלשהי, אזי f o id_M = f = id_N o f (כאשר "o" מייצג פעולת הרכבת פונקציות). בפרט, id_M הוא איבר יחידה של המונואיד הכולל את כל הפונקציות מ-M על M.

באלגברה לינארית

מעל מרחב וקטורי מממד סופי אפשר לייצג כל העתקה לינארית באמצעות מטריצה. במרחב וקטורי מממד סופי n מיוצגת העתקת הזהות על ידי מטריצת היחידה ${\displaystyle I_{n}}$ שצורתה

${\displaystyle I_{n}={\begin{bmatrix}1&0&\cdots &0\\0&1&\cdots &0\\\vdots &\vdots &\ddots &\vdots \\0&0&\cdots &1\end{bmatrix}}}$

זוהי מטריצה שבה כל איברי האלכסון הראשי הם 1 ושאר האיברים הם 0.