המכשפה של אנייזי

אנימציה המתארת את יצירת המכשפה של אנייזי

המכשפה של אנייזי (או עקומת אנייזי) היא עקומה שמשוואתה היא $y={\frac {8a^{3}}{x^{2}+4a^{2}}}$ , כאשר עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a} קבוע.

העקומה קרויה על שם המתמטיקאית האיטלקית בת המאה ה-18, מריה גאטנה אנייזי, שעסקה בעקומה בספרה משנת 1748, אף שהעקומה נחקרה עוד בשנת 1630 על ידי פייר דה פרמה.

תיאור גאומטרי לעקומה

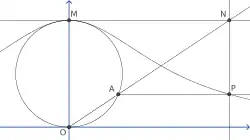
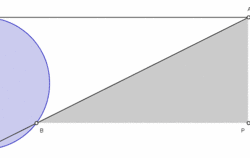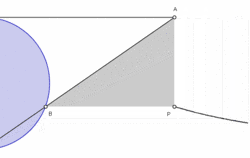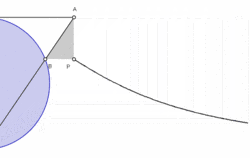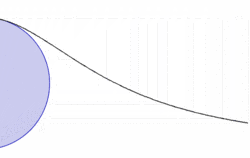
הסבר ליצירתה של המכשפה של אנייזי, שהיא העקומה המחברת את הנקודות עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle P,M} בשרטוט זה

על מעגל נתון נבחר זוג נקודות אנטיפודיות (נקודות שביניהן עובר קוטר) $O,M$ .

בהינתן על המעגל נקודה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle A\ne O} , נסמן עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle N} את מפגש הישר עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle OA} עם המשיק למעגל בנקודה $M$ .

נגדיר עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle P} כנקודת המפגש של הישר העובר דרך עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle N} ומקביל לקוטר $OM$ עם הישר העובר דרך עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle A} ומקביל למשיק $MN$ .

המקום הגאומטרי של כל הנקודות עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle P} המתאימות לכל הנקודות עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle A} על פני כל המעגל הנתון הוא המכשפה של אנייזי.

תיאור אנליטי לעקומה

מהתיאור הגאומטרי של דרך בניית העקומה ניתן לעבור לתיאור פרמטרי שלה.

אם מציבים את המעגל כך ש-עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle O} ראשית הצירים, $M$ על ציר $y$ , ורדיוס המעגל עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a} (כלומר עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle OM=2a} ), אז העקומה מוגדרת על ידי הנוסחאות:

{\begin{aligned}x&=2a\tan(\theta )\\y&=2a\cos(\theta )^{2}\end{aligned}}

כאשר עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \theta\,} היא הזווית הגדלה עם כיוון השעון שבין הקטעים $OM,OA$ .

מהתיאור הפרמטרי ניתן לקבל את משוואת העקומה בקואורדינטות קרטזיות:

y={\frac {8a^{3}}{x^{2}+4a^{2}}}

בפרט, כאשר עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a=\tfrac12} מתקבלת העקומה הפשוטה $y={\frac {1}{1+x^{2}}}$ , שהיא – עד כדי כפל בקבוע – פונקציית צפיפות ההסתברות של התפלגות קושי.

תכונות

המכשפה של אנייזי עם הפרמטרים

a=1,2,4,8

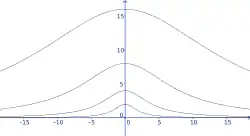
לעקומה יש מקסימום גלובלי כאשר עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle x=0} , ונקודת פיתול בנקודות עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (x,y)=\left(\pm\frac2{\sqrt3}a,\frac32a\right)} .

העקומה אסימפטוטית למשיק למעגל הנתון העובר דרך הנקודה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle O} (כאשר הנקודה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle O} נמצאת בראשית הצירים, משיק זה הוא ציר עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle x} ).

השטח הכלוא בין העקומה ובין משיק זה שווה לארבע פעמים שטחו של המעגל הנתון. כאשר רדיוס המעגל הנתון הוא עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a} , השטח הכלוא בין העקומה ובין המשיק הוא עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 4\pi a^2} . מרכז הכובד של שטח זה נמצא בנקודה $\left(0,{\tfrac {a}{2}}\right)$ .

נפח גוף הסיבוב של העקומה, הנוצר עם סיבובה סביב המשיק שהיא אסימפטוטית לו, הוא עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 4\pi^2a^3} .

היסטוריה

העקומה נחקרה על ידי פייר דה פרמה בשנת 1630. בשנת 1703 הציג לואיג'י גואידו גרנדי בנייה של העקומה. בשנת 1718 הציע גרנדי לקרוא לעקומה באיטלקית בשם averisera, בעקבות שמה האיטלקי של הפונקציה הטריגונומטרית versine בה השתמש לתיאור העקומה. בשנת 1748 פרסמה מריה גאטנה אנייזי את ספרה Instituzioni analitiche ad uso della gioventù italiana, שבו השתמשה בשם שהציע גרנדי. המתמטיקאי האנגלי ג'ון קולסון תרגם את ספרה של אנייזי לאנגלית וכינה את העקומה "Agnesi's Witch", כנראה עקב הדמיון בין המונח averisera לבין המילה האיטלקית avversiera שמשמעותה "אשת השטן" או "מכשפה".^[1] שם דומה משמש בשפות נוספות, ובאחרות ידועה העקומה במונחים שמשמעותם "המקום הגאומטרי של אנייזי" או "עקומת אנייזי".

היסטוריון המתמטיקה דירק יאן סטרייק (Struik) מייחס את הכינוי "מכשפה" למתמטיקאי בנג'מין ויליאמסון, בספרו Integral calculus משנת 1875. הסטטיסטיקאי סטיבן סטיגלר טוען שכבר גרנדי עצמו השתעשע במשחק המילים שבשם שהציע.

"המכשפה של אנייזי" הוא גם שמו של רומן מאת רוברט ספילר משנת 2006, שבו מורה מציג גרסה משלו להיסטוריה של המושג.^[2]

שימושים

בשלהי המאה ה-20 הפכה המכשפה של אנייזי מעקומה בעלת משמעות תאורטית בלבד, לכזו המופיעה בהקשרים פיזיקליים, ובהם התפלגותן של קרני אור^[3] וזרימה סביב מכשול חלק.^[4]

לקריאה נוספת

Gray, S.I.B. and Tagui Malakyan. "The Witch of Agnesi: A Lasting Contribution from the First Surviving Mathematical Work Written by a Woman," College Mathematics Journal, 30(4) (Sept. 1999), 258-268.

קישורים חיצוניים

ראו מדיה וקבצים בנושא זה בוויקישיתוף.

המכשפה של אנייזי, באתר MathWorld (באנגלית)
Witch of Agnesi, באתר MacTutor (באנגלית)

הערות שוליים

↑ ,Shirley B. Gray History of the Name "Witch", California State University, Los Angeles
↑ על הספר The Witch of Agnesi מאת רוברט ספילר, באתר Mathematical Fiction
↑ Sarah J. Greenwald, Applications to the witch, Appalachian State University
↑ William H. Snyder et al., The structure of strongly stratified flow over hills: dividing-streamline concept. J. Fluid Mech. (1985), vol. 162, pp. 249-288
Kevin G. Lamb, Numerical simulations of stratified inviscid flow over a smooth obstacle, J. Fluid Mech. (1994), vol. 260, pp. 1-22

This article is issued from Hamichlol. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] ,Shirley B. Gray History of the Name "Witch", California State University, Los Angeles

[hebrewRTL-ספילר-2] על הספר The Witch of Agnesi מאת רוברט ספילר, באתר Mathematical Fiction

[3] Sarah J. Greenwald, Applications to the witch, Appalachian State University

[4] William H. Snyder et al., The structure of strongly stratified flow over hills: dividing-streamline concept. J. Fluid Mech. (1985), vol. 162, pp. 249-288
Kevin G. Lamb, Numerical simulations of stratified inviscid flow over a smooth obstacle, J. Fluid Mech. (1994), vol. 260, pp. 1-22