מיון סלים

מיון סלים (באנגלית Bucket Sort) הוא אלגוריתם מיון של קבוצת מספרים ממשיים, או כל קבוצה אחרת, כאשר ידוע שהפיזור של האיברים אחיד, ואינו מתבסס על השוואות בין האיברים. בזכות מידע נוסף זה, סיבוכיות זמן הריצה של האלגוריתם אינה חסומה מלמטה על ידי ${\displaystyle \ \Omega (n\log n)}$ (כאשר ${\displaystyle \ n}$ הוא מספר האיברים שאותם רוצים למיין) כפי שחסומים אלגוריתמים המבוססים על השוואות, אלא היא ${\displaystyle \ O(N)}$, כאשר ${\displaystyle \ N}$ הוא גודל החסם של קבוצת המספרים. לכן האלגוריתם עדיף על אלגוריתמים מבוססי השוואות במקרים שבהם גודל החסם קטן יחסית למספר האיברים שאותם רוצים למיין. מיון סלים הוא מיון יציב, כלומר לא משנה את הסדר היחסי בין איברים זהים.

האלגוריתם

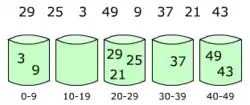
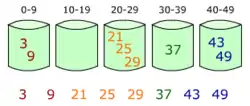
נניח שיש N מספרים. נחלק את הטווח שבין MIN ו-MAX ל-${\displaystyle \ O(N)}$ חלקים שווים. לפי ההנחה שהפיזור אחיד אז בכל חלק יש ${\displaystyle \ O(1)}$ איברים וניתן למיין כל חלק בסיבוכיות זמן ${\displaystyle \ O(1)}$. במספרים ממשיים למשל, ההחלטה לאיזה סל שייך מספר נקבעת על ידי חישוב יחיד של חילוק הערך שלו בגודל של כל סל, והערך השלם של התוצאה יקבע לאיזה סל להכניסו.

חישוב הסיבוכיות

עבור חלוקה של n איברים לתוך m סלים, בהנחה שהפונקציה המחלקת אורכת ${\displaystyle \ O(1)}$ לכל איבר אזי פעולת החלוקה אורכת ${\displaystyle \ O(N)}$ זמן, במקרה הגרוע, אם פיזור האיברים אינו אחיד, לסל אחד נכנסו ${\displaystyle \ O(N)}$ איברים ומיונם יארך ${\displaystyle \ O(N\log N)}$ והמעבר על שאר הסלים אורך ${\displaystyle \ O(M)}$ זמן, וסה"כ ${\displaystyle \ O(N\log N+M)}$ . לעומת זאת, בהנחה שאכן הפיזור אחיד, צריך למיין m תאים שבכל אחד מהם ${\displaystyle \ O(N/M)}$ איברים שלמיין כל אחד מהם אורך ${\displaystyle \ O((N/M)\log(N/M))}$ , וסה"כ אחרי שמכפילים ב-m תאים ומוסיפים את סיבוכיות החלוקה לתאים, צריך גם לקחת בחשבון גם מקרה ש-m הרבה יותר גדולה בסדר גודל מ-${\displaystyle \ N}$ ואורך יותר זמן המעבר על התאים ולכן צריך לחבר לסיבוכיות ${\displaystyle \ M}$ , זה אורך ${\displaystyle \ O(N\log(N/M)+M)}$ , במקרה האידאלי, שבו ${\displaystyle M=\Theta (N)}$ הסיבוכיות היא ${\displaystyle \ O(N)}$ .

קישורים חיצוניים

• סימולציה של מיון סלים
• מיון סלים בQueue