משפט הקוסינוסים
.gif)
משפט הקוסינוסים הוא משפט טריגונומטרי שמציין את הקשר בין צלעות משולש לאחת מזוויותיו. המשפט הוא הכללה של משפט פיתגורס למשולש כלשהו.
עבור משולש שצלעותיו הן עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a,b,c} והזווית שמול היא עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \gamma} , משפט הקוסינוסים קובע:
משפט פיתגורס מתקבל במקרה הפרטי שבו עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \gamma=90^\circ} ולכן .
היסטוריה
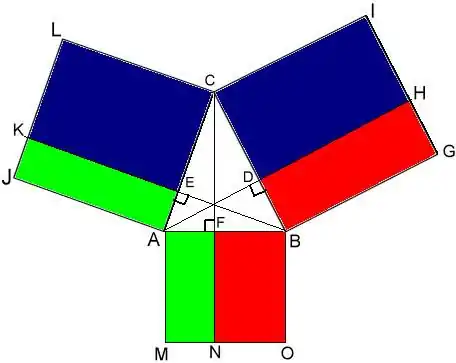
משפט הקוסינוסים מופיע כבר בספר 'יסודות' של אוקלידס מהמאה ה-3 לפנה"ס. הספר מכיל גרסה גאומטרית, ללא שימוש בפונקציות טריגונומטריות (כיוון שטרם הוגדרו). המשפט מופיע בכרך 2 של ה'יסודות' כמשפט 12 עבור משולש קהה-זווית וכמשפט 13 עבור משולש חד-זווית.
בציור משמאל, גרסת המשפט עבור משולש חד-זווית: .
מכיוון ש-עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle S_{\color{blue}DHIC}=BC\cdot AC\cdot\cos(ACB)} מתקבל משפט הקוסינוסים בגרסתו המוכרת. גרסה זו נוסחה בימי הביניים בעקבות פיתוחו של ענף הטריגונומטריה על ידי מתמטיקאים מוסלמים.
בתחילת המאה ה-10 האסטרונום והמתמטיקאי המוסלמי אל-בתאני הכליל את המשפט לגאומטריה ספירית. הכללה זו אפשרה לו לחשב את המרחק הזוויתי בין כוכבים.
המתמטיקאי ג'משיד אל-קאשי מסמרקנד בן המאה ה-15 חישב ערכים של פונקציות טריגונומטריות. חישוביו הפכו את משפט הקוסינוסים ממשפט תאורטי למשפט שימושי. בצרפתית משפט הקוסינוסים נקרא משפט אל-קאשי.
הוכחות
הוכחה טריגונומטרית
- נעביר גובה לצלע (ראו ציור משמאל)
- (השוויון נכון גם עבור משולש קהה זווית. שם האנך חותך את מחוץ למשולש וקוסינוס הזווית הקהה הוא שלילי).
- נכפיל את השוויון הקודם ב- ונקבל .
- באותו אופן מקבלים עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a^2=ac\cos(\beta)+ab\cos(\gamma)\ ,\ b^2=bc\cos(\alpha)+ab\cos(\gamma)} .
- מחיבור שתי המשוואות הנ"ל נקבל .
- לאחר העברת אגפים נקבלל עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle ac\cos(\beta)+bc\cos(\alpha)=a^2+b^2-2ab\cos(\gamma)} .
- לפי השלב השני בהוכחה, אגף שמאל של המשוואה האחרונה שווה ל-עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle c^2} ומתקבל משפט הקוסינוסים: עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle c^2=a^2+b^2-2ab\cos(\gamma)} .
הוכחה זו כאמור, נכונה עבור משולש כלשהו. בהוכחות רבות הנעזרות בטריגונומטריה, נעשית הפרדה בין משולשים חדי-זווית למשולשים קהי-זווית.
שימוש במשפט פיתגורס
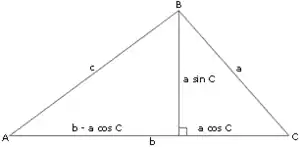
ניקח משולש בעל צלעות עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a,b,c} ובעל זוויות עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \alpha,\beta,\gamma} ממול לכל צלע בהתאמה. נוריד גובה מקודקוד הזווית עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \beta} לצלע . את המשוואה נקבל באמצעות משפט פיתגורס על המשולש ישר הזווית השמאלי:
- עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \begin{align}c^2&=\bigl(a\sin(\gamma)\bigr)^2+\bigl(b-a\cos(\gamma)\bigr)^2\\&=a^2\sin(\gamma)^2+b^2-2ab\cos(\gamma)+a^2\cos(\gamma)^2\\&=a^2\bigl(\sin(\gamma)^2+\cos(\gamma)^2\bigr)+b^2-2ab\cos(\gamma)\\&=a^2+b^2-2ab\cos(\gamma)\end{align}}
היות ש: .
שימוש במשפט תלמי
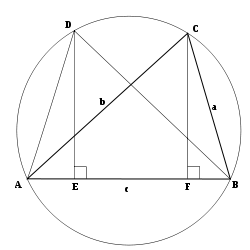
את שצלעותיו עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle BC=a,AC=b,AB=c} , נחסום במעגל, כפי שניתן לראות בשרטוט משמאל.
נבנה החופף למשולש המקורי: . מהקודקודים נעביר גבהים החותכים את הצלע עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle AB} בנקודות עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle E,F} בהתאמה.
- עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \begin{align}& BF=AE=BC\cos(\sphericalangle CBA)=a\cos(\sphericalangle CBA)\\&DC=EF=AB-2BF=c-2a\cos(\sphericalangle CBA)\end{align}}
כעת, ממשפט תלמי נקבל:
- עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \begin{align}&AD\cdot BC+AB\cdot DC=AC\cdot BD\\&a^2+c\bigl(c-2a\cos(\sphericalangle CBA)\bigr)=b^2\\&a^2+c^2-2ac\cos(\sphericalangle CBA)=b^2\end{align}}
שימוש באנליזה וקטורית
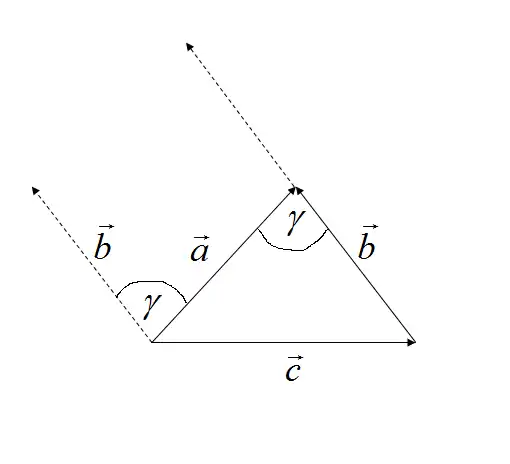
את המשפט קל להוכיח באמצעות חשבון וקטורים. וקטור הוא גודל לינארי מופשט הקיים במרחב וקטורי. על וקטורים במישור עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \R^2} ניתן לחשוב כעל חצים בעלי אורך וכיוון, ובאמצעותם לייצג צורות גאומטריות, ובפרט מצולעים כגון משולש.
קל לראות מהאיור כי .
נשתמש במכפלה סקלרית ונקבל:
- עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle c^2=\vec c\cdot\vec c=(\vec a-\vec b)\cdot(\vec a-\vec b)=\vec a\cdot\vec a+\vec b\cdot\vec b-2\vec a\cdot\vec b=a^2+b^2-2ab\cos(\gamma)}
שכן הזווית עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \gamma} שמול הצלע במשולש שווה לזווית בין הווקטורים עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \vec a,\vec b} (שכן הן זוויות בין ישרים מקבילים הנוצרים מהעתקה מקבילה של הווקטור ).
ראו גם
קישורים חיצוניים
- משפט הקוסינוסים, באתר MathWorld (באנגלית)

רישיון cc-by-sa 3.0