מעגל חוסם
בגאומטריה של המישור, מעגל חוסם של מצולע הוא מעגל העובר דרך כל הקודקודים של המצולע. בין המצולעים שיש להם מעגל חוסם: כל המשולשים, כל המלבנים, וכל המצולעים המשוכללים. מצולע שיש לו מעגל חוסם נקרא מצולע ציקלי.
המעגל החוסם משולש
במשולש, מרכז המעגל החוסם הוא הנקודה שבה נפגשים שלושת האנכים האמצעיים של הצלעות. הסיבה לכך היא שאנך האמצעים הוא המקום הגאומטרי של הנקודות שמרחקיהן מקצות הקטע שווים זה לזה, ומרחקו של המרכז מן הקודקודים, העומדים בקצותיה של כל צלע, הוא קבוע.
מיקומו של מרכז המעגל החוסם במשולש תלוי בסוג המשולש. במשולש חד-זווית המרכז בתוך המשולש, במשולש ישר-זווית המרכז נמצא באמצע היתר (זהו אחד הנוסחים של משפט תלס), ובמשולש קהה-זווית המרכז מחוץ למשולש.
_Circumscribed.svg.png.webp) במשולש חד-זווית, מרכז המעגל החוסם בתוך המשולש
במשולש חד-זווית, מרכז המעגל החוסם בתוך המשולש- במשולש קהה-זווית, מרכז המעגל החוסם מחוץ למשולש
מרכז המעגל החוסם של משולש נמצא על קו ישר אחד עם מפגש התיכונים ועם מפגש הגבהים; הישר המחבר את הנקודות נקרא ישר אוילר.
שלוש נקודות הנמצאות על ישר אחד אינן יוצרות משולש במובן המקובל של המילה, אבל אפשר להתייחס לישר המונח עליהן כאילו היה המעגל החוסם - "מעגל ברדיוס אינסופי". נקודות הקרובות למצב כזה עשויות לגרום לאי-יציבות בחישוב המעגל החוסם.
משפט אוילר, הקרוי על שמו של המתמטיקאי לאונרד אוילר, קובע כי המרחק d בין מרכז המעגל החוסם ומרכז המעגל החסום של משולש מקיים: עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle d^2 = R\cdot(R - 2r)} , כאשר R הוא רדיוס המעגל החוסם ו- r הוא רדיוס המעגל החסום. מנוסחה זו נובע כי: .
הזוויות בין הישר המשיק למעגל החוסם, בקודקוד A, לבין צלעות המשולש, שוות לזוויות B ו- C.
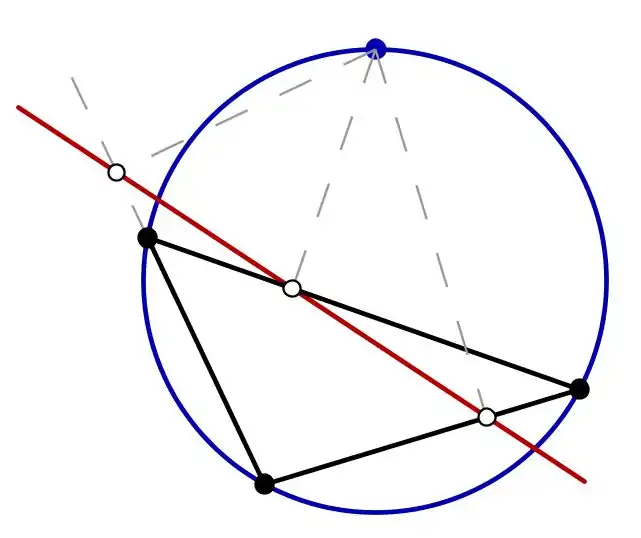
נקודה P נמצאת על המעגל החוסם אם ורק אם שלושת ההיטלים שלה על צלעות המשולש או המשכיהן נמצאים על ישר אחד. ישרים אלו, שהתגלו על ידי William Wallach ב-1797, קרויים בטעות ישרי סימסון, על-שם Robert Simson, 1687-1768[1].
הקוטר והמרכז של המעגל החוסם
נסמן ב-עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a,b,c} את צלעות המשולש, וב-עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \alpha} את הזווית שמול עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a} . לפי משפט הסינוסים, עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a=2Rsin(\alpha )} , ולכן שטח המשולש נתון לפי השוויון עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle S = \frac{1}{2}bc \sin(\alpha) = \frac{abc}{4R}} . מכאן שבכל משולש מתקיים היחס . את רדיוס המעגל החוסם אפשר לחשב ישירות מאורכי הצלעות a, b ו- c, לפי הנוסחה , כאשר עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ S = \sqrt{s(s-a)(s-b)(s-c)}} הוא שטח המשולש (לפי נוסחת הרון), ו- חצי ההיקף. קוטרו של מעגל פיירבך הוא מחצית מזה של המעגל החוסם.
בקואורדינטות קרטזיות, המעגל החוסם של משולש שקודקודיו בנקודות עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mathbf{A} = (A_x,A_y)} , עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mathbf{B} = (B_x,B_y)} ו- הוא האוסף של נקודות עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ v=(v_x,v_y)} המקיימות את המשוואות , עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle |\mathbf{A}-\mathbf{u}|^2 - r^2 = 0} ו- עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle |\mathbf{B}-\mathbf{u}|^2 - r^2 = 0} ו- עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle |\mathbf{C}-\mathbf{u}|^2 - r^2 = 0} , שמהן נובע גם ש- הוא מרכז המעגל החוסם. כשהופכים את המשוואות למערכת המשוואות הלינארית, מתברר שהן שקולות לכך שלמטריצה הריבועית עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \begin{vmatrix} |\mathbf{v}|^2 & -2v_x & -2v_y & -1 \\ |\mathbf{A}|^2 & -2A_x & -2A_y & -1 \\ |\mathbf{B}|^2 & -2B_x & -2B_y & -1 \\ |\mathbf{C}|^2 & -2C_x & -2C_y & -1 \end{vmatrix}} תהיה דטרמיננטה אפס. מנוסחת קרמר מתקבל הפתרון עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \quad S_x=\frac{1}{2}\det\begin{vmatrix} |\mathbf{A}|^2 & A_y & 1 \\ |\mathbf{B}|^2 & B_y & 1 \\ |\mathbf{C}|^2 & C_y & 1 \end{vmatrix},\quad S_y=\frac{1}{2}\det\begin{vmatrix} A_x & |\mathbf{A}|^2 & 1 \\ B_x & |\mathbf{B}|^2 & 1 \\ C_x & |\mathbf{C}|^2 & 1 \end{vmatrix},} , , ואז מתקבל המרכז ורדיוס המעגל עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ \sqrt{ab+|S|^2}/a} . חישוב דומה מוביל לנוסחאות הכדור החוסם של ארבעון.
בקואורדינטות בריצנטריות, המעגל החוסם הוא אוסף הנקודות עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ x:y:z} המקיימות עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ \frac{1}{x}+\frac{1}{y}+\frac{1}{z} = 0} . מרכז המעגל בקואורדינטות אלה הוא עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ a^2(-a^2 + b^2 + c^2) : b^2(a^2 - b^2 + c^2) : c^2(a^2 + b^2 - c^2)} .
מעגל חוסם של מרובע

מרובע הוא ציקלי (כלומר, יש לו מעגל חוסם), אם ורק אם הסכום של כל זוג זוויות נגדיות הוא 180 מעלות.
מעגל עוטף מינימלי
לא לכל מצולע יש מעגל חוסם, שהרי הקודקודים אינם חייבים להיות מונחים על מעגל אחד. עם זאת, לכל מצולע יש מעגל עוטף מינימלי, שהוא המעגל הקטן ביותר הכולל בתוכו את המצולע (לבניית המעגל העוטף המינימלי יש אלגוריתם לינארי). המעגל החוסם עשוי להיות גדול מן המעגל העוטף המינימלי, למשל עבור משולש קהה זווית, שקוטר המעגל העוטף המינימלי שלו שווה לצלע הגדולה של המשולש.
מעגל חוסם במצולע משוכלל
במצולע משוכלל, מרכז המעגל החוסם מתלכד עם מרכז המעגל החסום.
נסמן:
- n - מספר הצלעות של המצולע המשוכלל
- t - אורך הצלע במצולע המשוכלל
- R - רדיוס המעגל החוסם
- r - רדיוס המעגל החסום.
מתקיים:
- עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ t = 2r \tan \frac \pi n = 2R \sin \frac \pi n}
- עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ r = \frac 1 2 t \cot \frac \pi n = R \cos \frac \pi n}
ראו גם
- מעגל חסום
- קבוע קפלר באוקמפ
הערות שוליים
- ↑ Geometry Revisited, Coxeter and Greitzer; סעיף 2.5