ציקלואידה

יצירת ציקלואידה

ציקלואידה היא צורה גאומטרית המתארת את מסלולה של נקודה קבועה על גבי מעגל המתגלגל (ללא החלקה) על קו ישר.

אורך העקומה הוא פי 8 מרדיוס המעגל היוצר, והשטח הכלוא בינה לבין הישר הוא פי שלושה משטח המעגל.

ציקלואידה הפוכה היא המסלול הפותר שתי בעיות ידועות העוסקות במציאת עקום גאומטרי תחת השפעת כבידה אחידה (ללא חיכוך):

1. בעיית הברכיסטוכרון (הזמן הקצר ביותר)
2. בעיית הטאוטוכרון (הזמן איננו תלוי בנקודת ההתחלה)

משוואות

ציקלואידה שנוצרה על-ידי מעגל שרדיוסו 2

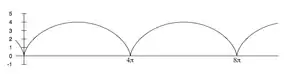
ציקלואידה העוברת דרך ראשית הצירים, הנוצרת בידי מעגל בעל רדיוס ${\displaystyle r}$ , ניתנת לתיאור פרמטרי בקואורדינטות קרטזיות על-ידי המשוואות:

${\displaystyle {\begin{aligned}x&=r{\big (}t-\sin(t){\big )}\\y&=r{\big (}1-\cos(t){\big )}\end{aligned}}}$

כאשר ${\displaystyle t}$ פרמטר ממשי, המייצג את גודל הזווית ברדיאנים בה הסתובב המעגל היוצר. עבור כל ${\displaystyle t}$ נתון, מרכז המעגל היוצר שוכן בנקודה ${\displaystyle (rt,r)}$ .

זוהי עקומה רציפה וחלקה (גזירה אינסוף פעמים) בכל מקום פרט לנקודות המפגש עם ציר ${\displaystyle x}$ , שם היא איננה גזירה. בנקודות בהן היא גזירה מתקיים:

${\displaystyle \left({\frac {dy}{dx}}\right)^{2}={\frac {2r}{y}}-1}$

שטח

השטח הכלוא תחת קשת ציקלואידה יחידה, מתקבל מהמשוואות שלמעלה על-ידי:

${\displaystyle 0\leq t\leq 2\pi }$

השטח הכלוא מתחת לגרף הוא האינטגרל: ${\displaystyle {\begin{aligned}A=\int \limits _{t=0}^{t=2\pi }y\,dx\end{aligned}}}$

התוצאה מתקבלת על ידי החלפת משתנים, לפי המשוואות שלמעלה: ${\displaystyle {\frac {dx}{dt}}=r{\bigl (}1-\cos(t){\bigr )}}$ , נקבל:

${\displaystyle {\begin{aligned}A=\int \limits _{t=0}^{t=2\pi }y\,dx=\int \limits _{t=0}^{t=2\pi }r^{2}{\big (}1-\cos(t){\big )}^{2}dt=r^{2}\left({\frac {3t+\sin(t){\big (}\cos(t)-4{\big )}}{2}}\right){\Bigg |}_{t=0}^{t=2\pi }=3\pi r^{2}\end{aligned}}}$

קיבלנו כי שטחה של הציקלואידה הוא פי שלושה משטח המעגל היוצר אותה.

תוצאה זו ניתן לקבל גם בעזרת עקרון קאוואליירי (שיטה דומה פותחה על-ידי ז'יל פרסון דה רוברוואל).

אורך הקשת

הפיתוח למציאת אורך קשת הציקלואידה הוא:

${\displaystyle {\begin{aligned}S=\int \limits _{0}^{2\pi }{\sqrt {\left({\frac {dy}{dt}}\right)^{2}+\left({\frac {dx}{dt}}\right)^{2}}}dt=r\int \limits _{0}^{2\pi }{\sqrt {2-2\cos(t)}}\,dt=2r\int \limits _{0}^{2\pi }\left|\sin \left({\frac {t}{2}}\right)\right|dt=4r\int \limits _{0}^{\pi }\sin \left({\frac {t}{2}}\right)dt=8r\end{aligned}}}$

ראו גם

• קרדיואידה
• אסטרואידה
• דלתואידה
• בעיית הברכיסטוכרון
• בעיית הטאוטוכרון