שידור מוצפן

בקריפטוגרפיה, סכימת שידור מוצפן (Broadcast Encryption) היא טכניקה לשידור יעיל של תוכן מוצפן לקבוצה דינאמית של משתמשים מורשים באופן שרק הם יוכלו לפענחו. כלומר כל המשתמשים שברשותם מקלט מתאים מסוגלים לקלוט את התוכן המשודר, אך רק קבוצה של משתמשים מורשים תוכל ליהנות ממנו, בעוד שהיתר אמורים לראות תוכן בלתי קריא. לעיתים נוח להתייחס לזה כאל 'סכימת ביטול' שמטפלת בצורך למנוע ממקלט אחד או יותר מלקלוט שידור מסוים.

שידור מוצפן לעיתים משולב עם "מנגנון מעקב" שמאפשר להתחקות אחר חשיפת תוכן בלתי חוקית או הפרת זכויות. במיוחד איתור וזיהוי מקור החשיפה, כך שהמערכת תוכל להגיב בהתאם. בדרך זו אפשר להתגונן מפני העתקה בלתי חוקית או שימוש בהתקנים לא חוקיים כמו מפענח פיראטי. יישומים אפשריים של שידור מוצפן כוללים:

• שלם וצפה; שיטות שידור בתשלום של תוכן אחיד למשתמשים מרובים.
• רב-נתיב; פרוטוקול תקשורת לניתוב מידע יחיד לנקודות מרובות.
• וידאו על פי דרישה; שירות אינטראקטיבי להעברת תכנים לפי דרישה.
• הזרמת מדיה; טכניקות העברת מדיה רציפה ומתמשכת על ידי ספקי תוכן.
• זכויות יוצרים; הגבלת גישה והגנה מפני העתקה פיראטית של מדיה דיגיטלית כמו תקן Advanced Access Content System.
• שימוש אפשרי נוסף הוא אבטחת שיתוף מידע במחשוב ענן.

היישומים השונים מכתיבים גישות שונות לניהול ועדכון רשימת המשתמשים הלגיטימיים. משתמשים מוסרים מהרשימה עקב אי תשלום, תפוגה של מנוי או שימוש בלתי הולם. מקרה מיוחד של הבעיה נקרא "State-less", כלומר משתמש לגיטימי לא יוכל להקליט את היסטוריית התכנים שקיבל כדי לשנות את מעמדו באופן שיאפשר לו לראות תכנים בלתי מורשים. במקרה זה ההחלטה האם משתמש רשאי לקבל תוכן מבוקש מתבססת רק על השידור הנוכחי והקונפיגורציה הראשונית שלו. 'משתמש חסר מעמד' נחוץ במקרים בהם השידור מופץ להתקנים שאינם בהכרח מקוונים, כגון נגן DVD במקרה זה ה"שידור" הוא בעצם התקליטור.

הגדרות כלליות

הבעיה הכללית שנקראת בעיית שידור מוצפן מתעוררת בתרחישים שונים כמו העברת תכנים בסגנון שלם וצפה והיא כדלהלן: שרת מרכזי מעוניין לשדר תוכן רב לקבוצה גדולה של מקלטים, כך שרק תת-קבוצה מוגדרת מראש תוכל לפענח את התוכן המשודר. דרך נאיבית לפתור את הבעיה היא להפיץ מראש לכל המשתמשים הרשומים במערכת מפתחות הצפנה סודיים, כל משתמש מקבל מפתח שונה. את המפתח הסודי אפשר להעביר בדרך בטוחה כלשהי או להטמיעו בתוך חומרת המקלט באופן בטוח. כמובן שזה לא מעשי להצפין ולשדר את התוכן עצמו מספר מרובה של פעמים עם מפתח אחר בכל פעם אלא במקום זאת, השרת מכין תחילה מפתח שיחה, מצפין את גוף התוכן, מצפין את המפתח איתו השתמש במספר הפעמים הדרוש עבור כל משתמש מורשה (עם המפתח הסודי המשותף לו ולשרת) ואז משדר את כל המפתחות המוצפנים יחד עם התוכן המוצפן, רק המשתמשים המחזיקים במפתחות המתאימים יוכלו לחלץ את מפתח ההצפנה מהמידע הנלווה ולפענח את התוכן. דרך זו אינה יעילה במיוחד בעיקר ברשת מרובת משתתפים כי נפח המידע שהשרת צריך לשדר מלבד התוכן גדל משמעותית, כלומר גודל המפתחות המוצפנים כפול מספר המשתמשים.

אפשר לחלק את המשתמשים הרשומים לתת-קבוצות (למשל תת-קבוצה אפשרית היא כל המשתמשים שהזמינו תוכן מסוים) ולהקצות מראש לכל תת-קבוצה אפשרית מפתח הצפנה מתאים, כך שהשרת צריך להצפין ולשדר את התוכן רק פעם אחת עבור תת-הקבוצה המתאימה ואינו נדרש לשדר מלבד התוכן שום דבר. אולם במקרה כזה כל משתמש רשום יאלץ להחזיק בכמות עצומה של מפתחות (מפתח אחד עבור כל תת-קבוצה אפשרית שהוא עשוי להיות חבר בה). המטרות הן למצוא דרך מאוזנת שבה כמות המפתחות שמשתמש בודד צריך להחזיק תהיה המינימלית האפשרית, שתעבורת הרשת לא תגדל משמעותית עקב התרחבות המידע המוצפן וכן כמות העבודה שתדרש מכל משתמש כדי לפענח את התוכן שיקבל לא תהיה גבוהה. בכללות התכונות המינימליות הדרושות ממערכת שידור מוצפן הן:

• רוחב פס נמוך; כלומר התרחבות מינימלית של התוכן עקב ההצפנה.
• דרישות אחסון נמוכות; שכל משתמש יאלץ להחזיק בכמות נמוכה ביותר האפשרית של מידע פרטי כמו מפתחות הצפנה.
• זמינות; אפשרות למצב של שידור "חסר מעמד" כך שהמשתמש אינו נדרש להיות מקוון כמו תקליטור.
• עמידות; תכונה חשובה של שידור מוצפן היא היכולת להתנגד לשיתוף פעולה או "קואליציה" של מספר משתמשים כנגד המערכת על מנת לקבל מידע בלתי מורשה.

בדרך כלל יש איזון בין הצורך בביטחון לעומת נוחות. לפעמים מתפשרים בביטחון השידור המוצפן על מנת להבטיח תעבורה גבוהה או תקורה נמוכה. על מנת להעריך או להשוות בין שיטות שידור מוצפן, צריך להגדיר מספר פרמטרים. קבוצת כל המשתמשים הרשומים במערכת מסומנת ב-עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mathcal{N}} ומכילה ${\displaystyle N=|{\mathcal {N}}|}$ חברים. הקבוצה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mathcal{R}\subset\mathcal{N}} היא תת-קבוצה המכילה עיבוד הנוסחה נכשל (שגיאת המרה. השרת ("https://en.wikipedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle r=|{\mathcal {R}}|} משתמשים בלתי מורשים (Revoked) שיש לבטל את תקפות מפתחות ההצפנה שלהם ולא לאפשר להם ליהנות מהתוכן (כגון, אם לא שילמו עבורו). עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle M} מייצג את התוכן המיועד לשידור במצבו הגלוי, אותו השרת צריך להצפין ולשדר באופן כזה שרק תת-הקבוצה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle u\in \mathcal{N}\setminus \mathcal{R}} (המורשים פחות המבוטלים) תוכל לפענחו, בעוד שקואליציה של עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle t} או פחות משתמשים החברים ב-${\displaystyle {\mathcal {R}}}$ לא תוכל. כמובן שאם אחד מהמשתמשים המורשים משתתף בקואליציה לא ניתן להגן על סודיות התוכן. מקרה כזה מוגדר כ'בגידה' והטיפול בה נעשה באמצעות מנגנון מעקב (Traitor tracing) להלן. מערכת שידור מוצפן כוללת שלושה מרכיבים עיקריים:

1. סכימת הקצאת מפתח. שהיא שיטת איתחול המייצרת ומפיצה מפתחות הצפנה סודיים לכל המשתמשים הרשומים.
2. אלגוריתם שידור. בהינתן תוכן עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle M} וקבוצה בלתי מורשית ${\displaystyle {\mathcal {R}}}$ מפיק ומשדר את עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle M'} לכל ${\displaystyle N}$ המשתמשים הרשומים.
3. אלגוריתם פענוח. משתמש לגיטימי שאינו נכלל בקבוצה ${\displaystyle {\mathcal {R}}}$ המקבל את עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle M'} משחזר את התוכן המקורי עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle M} באמצעות המפתח הסודי שברשותו משלב 1.

היסטוריה

נושא הצפנה משודרת הועלה כבר ב-1991 על ידי שמשון ברקוביץ שהציע שימוש בחלוקת סוד^[1] כדי לפתור את הבעיה. הגדרה הפורמלית ראשונה וניתוח יסודי של הבעיה ניתנו ב-1993 על ידי עמוס פיאט ומוני נאור^[2]. הם הציעו אלגוריתם המבוסס על עץ בינארי שמאפשר למנוע מכל מספר של משתמשים מלקבל תוכן כל עוד לא יותר מ-${\displaystyle k}$ מהם משתפים פעולה נגד המערכת. כמות המפתחות המוצפנים היא בסדר גודל של עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle O(k\text{ log}^2k)} וכל משתמש צריך לאחסן מספר מפתחות שהוא ביחס לוגריתמי ל-${\displaystyle k}$. כמות העבודה הנדרשת מכל משתמש היא ${\displaystyle O(r/k)}$ פענוחים. כמו כן הפרוטוקול תומך בסביבת Stateless ואינו דורש נוכחות (בלתי מקוון).

רעיון השימוש בלוגיקה של עץ היררכי הומצא בנפרד ב-1990 על ידי וולנר (Wallner)^[3] ווונג (Wong) שפיתחו שיטות לתקשורת בטוחה בתרחיש רב-נתיב (multicast) במצב מקוון. בשיטה זו שנקראת בקיצור LKH (להלן) יש צורך לשדר ${\displaystyle 2{\text{ log }}N}$ מפתחות בכל פעם שמעדכנים את הרשימה (מבטלים משתמש), כל משתמש נדרש לאחסן ${\displaystyle {\text{log }}N}$ מפתחות וכן כמות העבודה שכל משתמש נדרש לבצע היא ${\displaystyle {\text{log }}N}$ פעולות פענוח (בממוצע רק 1). הפרוטוקול בטוח ללא תלות ב-${\displaystyle k}$ אך כמות המידע המשודר היא עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle r\text{ log }N} שזה יחסית גבוה אלא אם כן כל משתמש יאחסן יותר מידע. הנושא נחקר על ידי רבים אחרים.

השיטה subset difference (להלן) שהוצעה ב-2002 על ידי נאור ולוצפיץ'^[4] היא הטובה ביותר למצב Statesless. לפי שיטה זו התוכן המשודר דורש רק עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 1.38r} הצפנות במקרה הממוצע כדי לבטל ${\displaystyle r}$ משתמשים, כמות האיחסון של כל מקבל היא ${\displaystyle \textstyle {\frac {1}{2}}{\text{ log}}^{2}N}$ מפתחות. אין הגבלה על ${\displaystyle r}$ וכן תהליך הקצאת המפתח הוא חישובי ולא מסתמך על תורת האינפורמציה. שמיר הלוי ואחרים הציעו שיפור לשיטה זו שנקרא LSD כמות האחסון מצטמצמת לפיה ל-${\displaystyle {\text{log}}^{1+\epsilon }N}$ וכמות התוכן היא בפקטור עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle r/\epsilon} , כאשר עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \epsilon } יכול 2.

שיטות ומבנים

להלן פירוט שלוש שיטות בסיסיות לפתרון בעיית שידור מוצפן שהמכנה המשותף שלהן בתהליך הקצאת המפתחות הוא השימוש במבנה דמוי עץ. מקצים מפתח ראשי לשורש העץ ולכל יתר הצמתים והעלים מקצים מפתחות בשיטת GGM שהוצעה על ידי גולדרייך, גולדווסר ומיקאלי שהיא סוג של פונקציה פסאודו-אקראית.

Subset Cover

הבסיס התיאורתי למשפחת האלגוריתמים Subset-Cover מתחיל במושג שהגו לראשונה פיאט ונאור^[5] שנקרא סכימת ביטול "k-resilient" הפועלת כך שבהינתן קבוצה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle U} של עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle n} חברים, הסכימה תהיה עמידה כנגד קואליציה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle S} של עד ${\displaystyle k}$ חברים. לשם כך מקצים מפתחות הצפנה סודיים ונפרדים עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle K_B} עבור כל תת-קבוצה ${\displaystyle B\subset U}$ אפשרית כאשר עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 0\le |B| \le k} , אותו מעבירים לכל משתמש ${\displaystyle u\in U-B}$ (לכל המשתמשים החברים ב-עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle U} אך אינם נמנים עם ${\displaystyle B}$). אפשר לדמות זאת באנלוגיה למצב שבו המפתחות נרשמים על גבי מצחם של כל המשתמשים, כל אחד יכול לראות את המפתחות של כולם למעט המפתח הרשום על מצחו. אם הקבוצה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle T} היא אוסף חברים מורשים, מפתח ההצפנה הסודי עבורם הוא XOR של כל המפתחות עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle K_B} כאשר עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle B\subset U-T} . כל קואליציה של ${\displaystyle S\leq k}$ חברים תחסר את המפתח עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle K_S} (המשויך להם) ולכן לא תוכל לחלץ את המפתח של עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle T} בתנאי שמתקיים עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle S\cap T=\emptyset} .

הסכימה המתוארת הוכחה בטוחה מהיבט תיאורתי אך אינה יעילה, כדי לכסות את כל האפשרויות, כל משתמש נדרש לאחסן ${\displaystyle \textstyle \sum _{i=0}^{k}{\binom {n}{k}}}$ מפתחות (לדוגמה; עבור עשרה משתמשים שמתוכם חמשה מבוטלים, כל משתמש נדרש לאחסן 638 מפתחות). במקרה הפרטי שבו עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle k=1} (כלומר רק משתמש אחד מבוטל) מספר המפתחות שכל אחד נדרש לשמור הוא ${\displaystyle n+1}$. אפשר לשפר את הסכימה על ידי הסתמכות על פונקציה חד-כיוונית ואז הביטחון אינו אבסולוטי אלא חישובי. מדמים את רשימת המשתמשים לעץ בינארי שכל עלה בו מתאים למשתמש אחד. מקצים מפתח אקראי לשורש העץ ולכל צומת מקצים רקורסיבית מפתח מתאים על ידי פונקציה פסאודו-אקראית עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f:\{0,1\}^\ell\mapsto\{0,1\}^{2\ell}} שמקבלת קלט מפתח של צומת אב ומפיקה פלט כפול באורכו, מחצית אחת מקצים לבן השמאלי והמחצית השנייה לבן הימני. היתרון שבשיטת בנייה זו הוא שכעת כל משתמש נדרש לדעת בעיקרון רק מפתח של אב קדום כלשהו שלו, כי המפתח שלו הוא תוצאה של הפעלת הפונקציה הפסאודו-אקראית באופן רקורסיבי במסלול מהשורש ועד לעלה שלו. כעת כדי לבטל עלים מסוימים מסירים את המסלולים המקשרים ביניהם לבין שורש העץ, כך למעשה נוצר "יער" של עיבוד הנוסחה נכשל (שגיאת המרה. השרת ("https://en.wikipedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle \lceil {\text{log }}n\rceil } תת-עצים, כל משתמש צריך לקבל כעת את מפתחות של כל שורשי תת-העצים. כעת אם המדיה מוצפנת עם XOR של כל המפתחות המשויכים למשתמשים שהוסרו, כל משתמש עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle x} יכול לחשב כל מפתח מלבד המפתח המשויך אליו ולכן אינו יכול לחלץ את המפתח לתוכן. המשתמשים המורשים לעומת זאת מקבלים את המפתח כשהוא מוצפן עם המפתח הפרטי שהם משתפים עם השרת.

דרך אחרת היא לבסס את הסכימה על בעיה מתורת המספרים דוגמת RSA. השרת מכין מפתח שורש שהוא ${\displaystyle n=pq}$, כפולה של שני ראשוניים גדולים, בוחר יוצר ${\displaystyle g}$ מסדר גבוה וכל משתמש עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle i} מקבל את עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle g_i=g^{p_i}} כאשר כל עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p_i} זרים הדדית. המפתח המשותף לקבוצה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle T} הוא עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle g_T=g^{p_T}\text{ mod }n} כאשר עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \textstyle p_T=\prod_{i\in T}p_i} ואז המשתמש עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle i} מחלץ את המפתח המשותף על ידי עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \textstyle g_T=g_i^{\prod_{j\in T-\{i\}}p_j}\text{ mod }n} כלומר חזקה של כל המפתחות למעט המפתח שלו. הוכח שהסכימה הזו בטוחה בהנחה שפירוק לגורמים היא בעיה קשה וכל מה שנדרש לאחסן הוא רק מפתח אחד.

בשתי הסכימות השרת אינו נדרש לשדר כלל מידע נלווה לתוכן המוצפן, כיוון שהמפתחות הוקצו מראש ובידי המשתמשים המידע הדרוש לחילוץ מפתח השיחה. אולם שיתוף פעולה של שני משתמשים מאפשר להם לשבור בקלות את המערכת. אלגוריתם Complete Subset Cover מרחיב את הרעיון הבסיסי לעמידות כנגד עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle k>1} מבוטלים וכן מצמצם את דרישות האחסון ברמת משתמש במחיר שהשרת ישדר לפני כל תוכן מוצפן מידע מסוים שנקרא "כותר". בכללות הוא מגדיר אוסף של תת-קבוצות עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle S_1,...,S_w} כאשר עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle S_j\subseteq\mathcal{N}} . מקצים מפתח סודי ארוך טווח (קבוע) עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle L_j} לכל עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle S_j} ולכל עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle u\in S_j} מקצים מידע פרטי עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle I_u} איתו הוא אמור לשחזר את עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle L_j} . בהינתן קבוצה ${\displaystyle {\mathcal {R}}}$ של משתמשים מבוטלים יתר המשתמשים ${\displaystyle {\mathcal {N}}\setminus {\mathcal {R}}}$ מחולקים לתת-קבוצות זרות עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle S_{i_1},...,S_{i_m}} כך שמתקיים:

${\displaystyle {\mathcal {N}}\setminus {\mathcal {R}}=\bigcup _{j=1}^{m}S_{i_{j}}}$.

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle K} מוצפן ${\displaystyle m}$ פעמים עם המפתחות ${\displaystyle L_{i_{1}},...,L_{i_{m}}}$ בהתאמה.

לצורך כך יש להגדיר שני פרימיטיבים קריפטוגרפיים: (1) צופן מהצורה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle F_K:\{0,1\}^*\mapsto \{0,1\}^*} להצפנת התוכן עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle M} עם עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle K} שצריך להיות חדש עבור כל תוכן. הצופן צריך להיות מהיר ולא אמור לגרום להתנפחות התוכן עקב ההצפנה. הוא יכול להיות צופן זרם בטוח כמו Salsa20. וכן (2) צופן מהצורה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle E_L\{0,1\}^\ell\mapsto\{0,1\}^\ell} עם מפתח ארוך-טווח עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle L} שהמרכז משתף עם כל משתמש בנפרד. יכול להיות צופן בלוקים כמו AES. מסיבות של יעילות רצוי ש-עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle K} יהיה קצר (להגנה על זכויות יוצרים אין צורך בהצפנה כבדה) ורק המפתח ארוך הטווח צריך להיות באורך מלא (בדרך כלל 128 סיביות). בגלל שאורך הכותר תלוי בגודל הבלוק של צופן הבלוקים, אפשר להשתמש בחלופה חסכונית כך; עיבוד הנוסחה נכשל (שגיאת המרה. השרת ("https://en.wikipedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle [{\text{Prefix}}_{|K|}E_{L}({\mathcal {U}})]\oplus K} במקום בלוק מלא. כאשר הביטוי עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \text{Prefix}_i(S)} פירושו עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle i} הסיביות הראשונות של הערך עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle S} וכן ${\displaystyle {\mathcal {U}}}$ הוא מחרוזת אקראית כלשהי באורך בלוק מלא.

CPRM/CPPM

Content Protection for Recordable Media and Pre-Recorded Media היא טכנולוגית ניהול זכויות דיגיטלי שפותחה ב-2001 על ידי 4C Entity (התאגדות של ארבעה ענקי אלקטרוניקה; IBM, אינטל, פנסוניק וטושיבה). CPRM/CPPM נועד בעיקר למצב 'חסר מעמד' (statelss). זהו מנגנון הכולל שיטות להגבלה ושליטה על מדיה דיגיטלית פיזית כמו תקליטורי DVD, כרטיסי זיכרון כמו SD או זיכרון הבזק בהתקן מארח (מחשב אישי או נגן).

מרכז רישוי כלשהו מפיץ רשימת מפתחות סודיים להטמעה בכל התקן בעת ייצורו. מרכז הרישוי מספק גם בלוק מפתח (MKB) שנועד לצריבה בכל מדיה מתאימה. בלוק המפתח (Media Block Key) למעשה נחשב מעין "כותר" המכיל טקסט-מוצפן של מפתח השיחה איתו הוצפנה המדיה. ההנחה היא שהבלוק ממוקם בשטח מיוחד שבו מתאפשרת כתיבה חד-פעמית בלבד. המדיה הצרובה על גבי התקליטור למעשה מקודדת במצב מוצפן כאשר מפתח ההצפנה מוסתר בכותר. כאשר המשתמש מכניס תקליטור, ההתקן מחלץ את מפתח השיחה מהכותר בעזרת המפתח הסודי המוטמע בו וכך מפענח את המדיה שעל גבי התקליטור.

האלגוריתם שמיישם CPRM הוא למעשה וריאציה של שיטת פיאט-נאור שנקראת סכימת Subset-Cover. הוא מגדיר טבלה עם עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle A} שורות ו-עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle C} עמודות, ומתייחסים לכל התקן (מקלט) כאל אוסף של עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle C} כניסות בטבלה, אחת בכל עמודה, כלומר עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle u=[u_1,...,u_C]} כאשר עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle u_i\in \{0,1,...,A-1\}} . אוסף כל תת-הקבוצות האפשריות עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle S_1,...,S_w} המוגדר על ידי האלגוריתם מתאים לאוסף התקנים שנמצאים באותה כניסה בעמודה נתונה. למשל עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle S_{r,i}} כולל את כל ההתקנים עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle u=[u_1,...,u_C]} כך ש-${\displaystyle u_{i}=r}$. עבור כל שורה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle i} ועמודה ${\displaystyle j}$ הסכימה מקצה מפתח המיוצג על ידי עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle L_{i,j}} . בכל התקן עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle u=[u_1,...,u_C]} מוטמע מידע פרטי (סודי) עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle I_u} הכולל עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle C} מפתחות ${\displaystyle L_{u_{1},1},L_{u_{2},2},...,L_{u_{C},C}}$.

עבור קבוצה ${\displaystyle {\mathcal {R}}}$ של התקנים "מבוטלים" (Revoked), האלגוריתם מחלק את ${\displaystyle {\mathcal {N}}\setminus {\mathcal {R}}}$ כך שכל תת-קבוצה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle S_{i,j}} מכוסה רק אם עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle S_{i,j}\cap\mathcal{R}=\emptyset} . בעוד שהסכימה מבטיחה שהתקן לא מאושר לא יכלל בכיסוי, יש סיכוי נמוך שהתקן מאושר לא יכלל גם הוא. כלומר ייתכן התקן לגיטימי שייחשב כלא תקף. בניגוד לשיטת נאור, תת-הקבוצות בסכימת CPRM/CPPM אינן זרות לגמרי ולכן הכיסוי אינו משולם. יתרה מזו הסיכוי שהתקן מאושר יפסל גדל ככל ש-${\displaystyle r}$ גדל (מספר ההתקנים המבוטלים).

לשם השוואה לשיטת נאור אם עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle C=\text{log }N} ו-עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle A=r} אזי מנגנון CPRM/CPPM דורש עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle r\text{ log }N} הצפנות, כמות האחסון במקלט או התקן עומדת על ${\displaystyle {\text{log }}N}$ מפתחות, וכמות החישוב הדרושה בצד ההתקן היא רק פעולת פענוח אחת. למשל ב-DVD בלוק המפתח MKB מכיל 3MB. חסרון נוסף הוא בעובדה ש-${\displaystyle r}$ מוגבל, כלומר מספר המכשירים המבוטלים המקסימלי שאפשר להגדיר בשיטה זו הוא בערך 10,000. בשיטת נאור אפשר להגיע ל-250,000.

LKH

תיאור עץ LKH

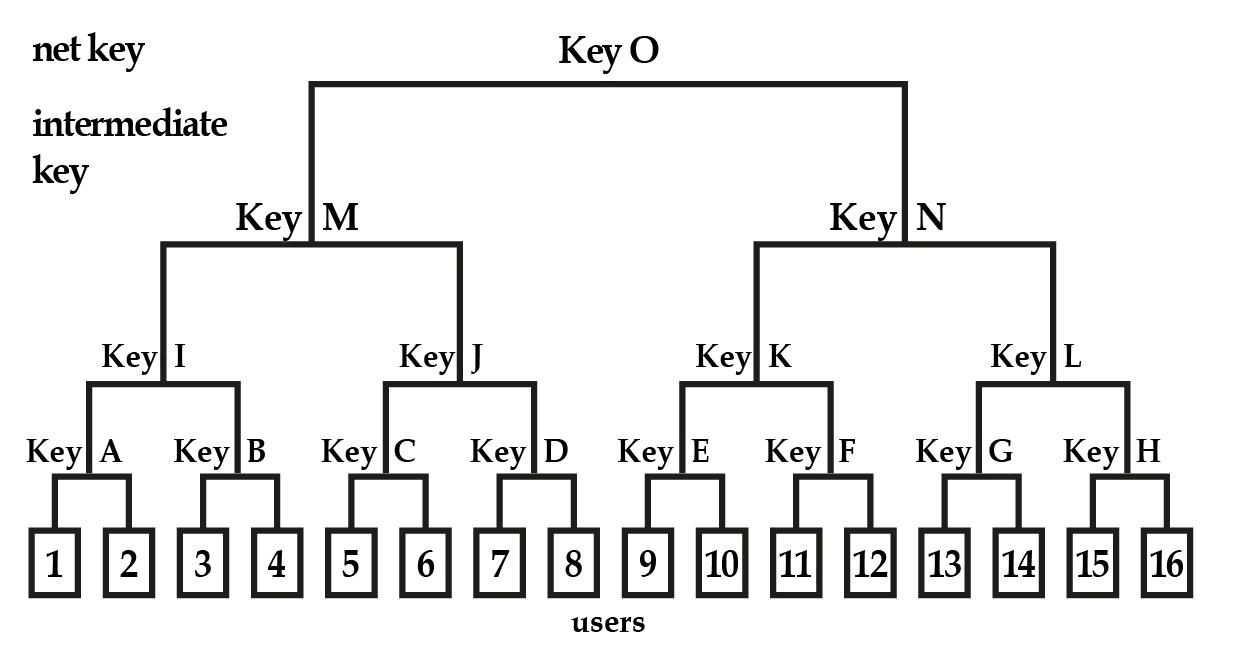
שיטת Logical-tree-hierarchy^[6] פותחה בעיקר לרב-נתיב במצב מקוון ונכללה בהצעה לתקן RFC-2627. המערכת מנהלת מפתח הצפנה משותף יחיד עבור קבוצת כל המשתתפים הפעילים עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mathcal{N}} שנקרא Net Key שמועבר אליהם באמצעות פרוטוקול העברת מפתח קריפטוגרפי כמו דיפי-הלמן. המערכת מוסיפה או מסירה משתתף (אחד בכל מהלך) על ידי אלגוריתם הקצאת מפתח שבו המערכת מחשבת ומקצה מפתחות הצפנה לכל המשתתפים הלגיטימיים. התהליך מנוהל על ידי שרת שמדווח לכל משתתפים על המהלכים שבוצעו. המשתתפים מיוצגים על ידי העלים בעץ בינארי מאוזן בגובה ${\displaystyle {\text{log }}N}$, לכל צומת עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle v_i} מוקצה מפתח ${\displaystyle K_{i}}$. כל משתתף עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle u_i} מקבל (בתהליך שנקרא Rekeying באמצעות המפתח הראשי) את כל המפתחות המשויכים לכל הצמתים במסלול המקשר משורש העץ לעלה שלו (לדוגמה בתרשים משתתף מספר 3 מקבל את המפתחות B,I,M). כדי להסיר את העלה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle u} מקצים מפתחות חדשים עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle K_i'} לכל הצמתים עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle v_i} לאורך המסלול המקשר מהעלה שהוסר ועד שורש העץ. כעת אם עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle v_i} הוא צומת הנמצא על המסלול, עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle v_j} צומת בן הנמצא על המסלול ו-עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle v_l} הוא צומת בן שאינו על מסלול. את המפתח עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle K_i'} של הצומת עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle v_i} מצפינים על ידי המפתחות עיבוד הנוסחה נכשל (שגיאת המרה. השרת ("https://en.wikipedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle K_{j}'} ו-עיבוד הנוסחה נכשל (שגיאת המרה. השרת ("https://en.wikipedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle K_{l}} (שים לב שהאחרון לא התעדכן) כלומר עיבוד הנוסחה נכשל (שגיאת המרה. השרת ("https://en.wikipedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle \langle E_{K_{j}'}(K_{i}'),E_{K_{l}}(K_{i}')\rangle } . במקרה ש-עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle v_i} הוא צומת אב של העלה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle u} מבצעים רק הצפנה אחת עם הצאצא של עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle u} . המפתחות החדשים המוצפנים משודרים לכל המשתתפים הפעילים. האלגוריתם מחייב העברה של ${\displaystyle 2{\text{ log }}N}$ מפתחות בכל פעולה כזו, כל משתתף נדרש לאחסן עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \text{log }N } מפתחות וכמות העבודה המקסימלית הנדרשת מכל משתתף היא ${\displaystyle {\text{log }}N}$ הצפנות (בממוצע נדרשת רק הצפנה אחת).

להלן טבלה להמחשה של תהליך הפצת מפתחות (Rekeying) של פרוטוקול LKH שתי העמודות האחרונות מתייחסות למספר המשתתפים שצריכים לקבל שידור בכל פעם שנוסף או מבוטל משתתף אחד בשידור.

מספר משתתפים	מעלה (${\displaystyle k}$)	אחסון פר משתתף	שידורי מפתח יחיד (${\displaystyle kd-1}$)	שידורי מפתחות מרובים עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle d(k-1)}
8	2	4	5	8
16	2	5	7	16
2048	2	12	21	2048
131072	2	18	33	131072

Subset Difference

תיאור עץ משתמשים בשיטת Subset Difference

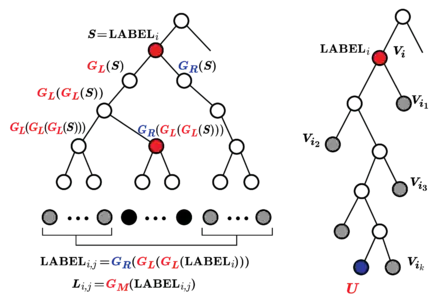
מבנה subset difference מגדיר אוסף של תת-קבוצות של משתמשים עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle S_1,...,S_w} כאשר ${\displaystyle S_{j}\in {\mathcal {N}}}$. לכל תת-קבוצה מקצים מפתח הצפנה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle L_j} , לכל משתמש עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle u} משייכים מידע סודי עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle I_u} איתו הוא יכול לחלץ את המפתחות של תת-הקבוצות אליהן הוא משויך. בהינתן הקבוצה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mathcal{R} } של משתמשים מבוטלים, יתר המשתמשים מחולקים לקבוצות זרות עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle S_{i_1},...,S_{i_m}} מהאוסף אשר 'מכסות' לגמרי את כל המשתמשים, כלומר כל משתמש חבר בלפחות קבוצה אחת כזו. מפתח שיחה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle K} מוצפן ${\displaystyle m}$ פעמים עם ${\displaystyle L_{i_{1}},...,L_{i_{m}}}$ והתוכן מוצפן עם עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle K} . כל המשתמשים משויכים לעלים בעץ בינארי מאוזן בגובה ${\displaystyle {\text{log }}N}$ אוסף הקבוצות עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle S_1,...,S_w} בהגדרה הוא מהצורה "קבוצה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle G_1} פחות הקבוצה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle G_2} " כאשר ${\displaystyle G_{2}\subset G_{1}}$. שתי הקבוצות מתאימות לעלים של שני תת-עצים בינאריים בהתאמה. לכן תת-קבוצה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle S} כלשהי מיוצגת על ידי שני צמתים בעץ הראשי עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle v_i,v_j} כך ש-עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle v_i} הוא אב קדום של עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle v_j} מסמנים זאת על ידי עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle S_{i,j}} (כמתואר בתרשים). העלה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle u} הוא בתת-קבוצה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle S_{i,j}} אם ורק אם הוא בתת-העץ שהשורש שלו הוא עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle v_j} . במילים אחרות עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle u\in S_{i,j}} אם עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle v_i} הוא אב קדום שלו אך לא עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle v_j} . הרעיון הוא שעבור כל תת-קבוצה ${\displaystyle {\mathcal {R}}}$ של משתמשים מבוטלים אפשר למצוא קבוצה של לכל היותר עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle s2-1} תת-קבוצות מהאוסף אשר מכסה את כל המשתמשים ב-עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mathcal{N} \setminus \mathcal{R}} .

אם יוקצה עבור כל משתמש מפתחות קבועים עבור אוסף כל הקבוצות מספר המפתחות עבור כל משתמש יהיה ${\displaystyle N}$. במקום זאת אפשר לצמצם את המידע הזה באופן כזה שרק ${\displaystyle \textstyle {\frac {1}{2}}{\text{ log}}^{2}N}$ מפתחות יאוחסנו, את המפתח הנכון המשתמש מחלץ באמצעות מבנה עץ דמוי GGM. לכל צומת מקצים שלושה מספרים אקראיים באמצעות מחולל פסאודו-אקראי בטוח, לכל צומת מצמידים תוויות המכילות את המספרים האקראיים עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle G_L} תווית עבור צד שמאל, עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle G_R} תווית עבור צד ימין ו-עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle G_M} תווית המייצגת את המפתח הסודי המשויך לעלה (כמתואר בתרשים). שים לב שלא ניתן לשחזר את המפתח של צומת נתון ללא ידיעת צומת האב.

בעת הפענוח המשתמש עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle u} מקבל את המחרוזת הבאה:

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \langle[i_1,...,i_m,E_{L_{i_1}}(K),E_{L_{i_2}}(K),...,E_{L_{i_m}}(K)],F_K(M)\rangle}

תחילה מוצא את תת-הקבוצה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle S_{i,j}} אליה הוא משויך ומחשב את המפתח המתאים עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle L_{i,j}} באמצעות הפעלת הפונקציה הפסאודו ראנדומלית על צמתי האב ${\displaystyle {\text{log }}N}$ פעמים. באמצעות טבלת גיבוב אפשר לצמצם את פעולת החיפוש של המשתמש ל-${\displaystyle O({\text{loglog }}N)}$. לאחר מכן כל מה שנדרש הוא פעולת פענוח אחת כדי לחלץ את התוכן המוצפן.

הפונקציות ${\displaystyle F_{K}}$ ו-עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle E_L} מייצגות אלגוריתמים להצפנה כאשר הראשון מומלץ שיהיה צופן זרם והאחרון צופן בלוקים כמו AES.

הערות שוליים