Twofish

Twofish הוא צופן בלוקים סימטרי שפותח ב-1998 בחברת Counterpane Labs על ידי צוות קריפטוגרפים בראשות ברוס שנייר, על מנת לשמש כמועמד לתקן ההצפנה המתקדם. דורג שלישי בחמשת המועמדים המובילים והפסיד לריינדל. האלגוריתם פועל על בלוקים בגודל 128 סיביות וטווח מפתח מ-128 עד 256 סיביות והוא ממוטב למעבדי 32 סיביות. בעת התחרות לתקן הוכרז על ידי NIST כמו לגבי יתר המועמדים המובילים שלא התגלו בו חולשות ולא ידוע על התקפה יעילה נגדו. הצופן נחשב כממשיכו של Blowfish וגם הוא חופשי לשימוש ואינו מוגן בזכויות יוצרים או פטנט. הוא בנוי בסגנון רשת פייסטל בשישה-עשר סבבים וכולל;

פונקציה חד-חד-ערכית ועל המיוצגת על ידי ארבע תיבות החלפה (S-box) לא ליניאריות תלויות מפתח, בגודל 8x8 סיביות.

הכפלה במטריצת MDS קיצור של maximum distance separable, שהיא פונקציה ליניארית קבועה 4x4 מעל שדה סופי $F_{2^{8}}$ וצמצום בפולינום פרימיטיבי קבוע.

התמרת פסבדו-הדמר PHT. פונקציית ערבוב הפועלת על זוגות משתנים בני 32 סיביות כדלהלן; בהינתן $a,b$ הפלט הוא $a'=(a+b){\mbox{ mod }}2^{32}$ ו- $b'=(a+2b){\mbox{ mod }}2^{32}$ .

הזזה מעגלית בסיביות (bitwise rotation), כלומר לאחר כל הזזה סיבית הגלישה הנפלטת מצד אחד מוחזרת מהצד השני.

הלבנה שהיא XOR עם 128 סיביות מהמפתח לפני הסבב הראשון ואחרי הסבב האחרון.

תהליך הרחבת מפתח המתואר להלן.

יישום ממוטב של האלגוריתם במחשב 32 סיביות צורך כ-18 מחזורי שעון לבית או 1820 מחזורי שעון במעבד 8 סיביות. Twofish ניתן ליישום בחומרה בעלות של 14,000 שערים. תהליך הרחבת המפתח וכן סבב ההצפנה מתחשב במגוון אפשרויות כדי לאפשר איזון בין ביצועים לבטחון בהתאם לצורך. ההתקפה הטובה ביותר הידועה כנגד האלגוריתם היא התקפת גלוי נבחר עם $2^{22.5}$ טקסטים ו- $2^{51}$ ניסיונות בחמשה סבבים בלבד. עם מפתח בגודל 128 סיביות יישום בתוכנה של Twofish איטי מעט בהשוואה לריינדל ואילו עם מפתח 256 סיביות קיים יתרון קל ל-Twofish.

שיקולי פיתוח

אלגוריתם Twofish פותח במיוחד לפי דרישות תקן ההצפנה של המכון הלאומי לתקנים וטכנולוגיה של ארצות הברית:

אורך הבלוק נקבע ל-128 סיביות.
אורכי מפתח נקבעו ל-128, 192 או 256 סיביות.
יעילות הן בחומרה והן בתוכנה.
גמישות; יישום במגוון אפשרויות על פלטפורמות שונות ועם אורכי מפתח שונים וכן התאמה לשימוש כצופן זרם, פונקציית גיבוב או קוד אימות מסרים.
מבנה פשוט המסייע ביישום ובניתוח האלגוריתם.
מהירות הצפנה של כ-500 מחזורי שעון בגרסה הממוטבת.
פעולות אלגבריות פשוטות שאינן מערימות קשיים ביישום בתוכנה או בחומרה.
בטחון; ההתקפה הטובה ביותר האפשרית כנגד האלגוריתם במלוא הסבבים תהיה בסיבוכיות של לא פחות מ- $2^{80}$ .

תיאור האלגוריתם

תרשים אלגוריתם Twofish. הסמל

\oplus

מייצג XOR והסמל

\boxplus

מייצג חיבור מודולו

2^{32}

. הפונקציה ROL מייצגת הזזה מעגלית שמאלה בסיביות לפי המציין התחתי ואילו ROR מייצג הזזה מעגלית ימינה

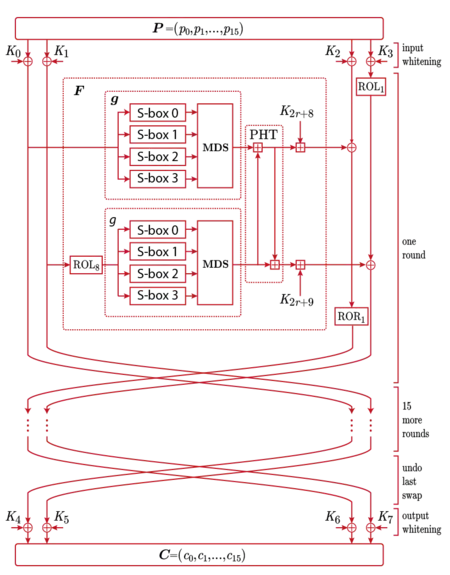
קלט: 128 סיביות טקסט קריא המיוצגים על ידי 16 בתים $p_{0},p_{1},...,p_{15}$ , מפתח $M$ בגודל 128, 192 או 256 סיביות.

פלט: 16 בתי צופן $c_{0},c_{1},...,c_{15}$ .

1. הקלט מפוצל לארבע מילים, $P_{0},P_{1},P_{2},P_{3}$ של 32 סיביות כל אחת לפי סדר בתים קטן (little-endian) כלומר הספרה הפחות משמעותית מוצבת בבית הראשון שבכתובת הזיכרון. הנוסחה היא:

\textstyle P_{i}=\sum _{j=0}^{3}p_{(4i+j)}\cdot 2^{8_{j}},\ \ \ \ \ i=0,...,3

(הערה: במעבד עם סדר בתים קטן (כמו בארכיטקטורת x86), בשפות C ו-C++‎ אין צורך בפעולת חישוב כלשהי בהמרה זו ובהמרה האחרונה בסעיף 6, כיוון שניתן להתייחס למצביע הקלט כאל כמצביע לשלם-32 במקום לבתים או להשתמש במבנה Union, כך שסיביות הקלט והפלט נותרות במקומן).

2. שלב הלבנה; מבצעים XOR עם 4 מילות מהמפתח המורחב $K$ (הכנת המפתח בהמשך):

R_{0,i}=P_{i}\oplus K_{i},\ \ \ \ \ i=0,...,3

3. בכל סבב מ-16 הסבבים, שתי המילים הראשונות $R_{0},R_{1}$ משמשות כקלט לפונקציה $F$ (להלן) שמקבלת כפרמטר גם את מספר הסבב, המילה השלישית $R_{2}$ מחוברת ב-XOR עם התוצאה הראשונה של $F$ ולאחר מכן מסובבת בהזזה מעגלית סיבית אחת ימינה. המילה הרביעית $R_{3}$ מסובבת בהזזה מעגלית שמאלה סיבית אחת ואז מחוברת ב-XOR עם התוצאה השנייה של $F$ . לאחר מכן שני החצאים מחליפים מקומות וחוזר חלילה. באופן פורמלי עבור $r=0$ עד $15$ מבצעים:

3.1 $(F_{r,0},F_{r,1})=F(R_{r,0},R_{r,1},r)$

3.2 $R_{r+1,0}={\mbox{ROR}}_{1}(R_{r,2}\oplus F_{r,0})$

3.3 $R_{r+1,1}={\mbox{ROL}}_{1}(R_{r,3})\oplus F_{r,1}$

3.4 $R_{r+1,2}=R_{r,0}$

3.5 $R_{r+1,3}=R_{r,1}$

כאן ROR מייצג Rotate Right שהיא פונקציית הזזה מעגלית לימין במספר סיביות לפי המציין התחתי ו-ROL מייצג Rotate Left.

4. מבצעים החלפה נוספת בין שני חצאי הקלט (למעשה מבטלים את ההחלפה מהסבב האחרון)

5. מבצעים הלבנה נוספת עם ארבע מילות מפתח מורחב נוספות. $C_{i}=R_{16,(i+2){\mbox{ mod }}4}\oplus K_{i+4},\ \ \ \ i=0,...,3$

6. התוצאה מומרת בחזרה ל-16 בתים לפי אותו סדר בתים: $c_{i}=\left\lfloor {\frac {C_{\left\lfloor i/4\right\rfloor }}{2^{8(i{\mbox{ mod }}4)}}}\right\rfloor {\mbox{ mod }}2^{8},\ \ \ \ i=0,...,15$

פונקציה F

הפונקציה $F$ מקבלת שלושה פרמטרים: שתי מילים $R_{0},R_{1}$ ומספר הסבב $r$ שמהווה אינדקס לערך המתאים במפתח המורחב. $R_{0}$ משמש קלט לפונקציית $g$ שמתוארת להלן המחזירה את $T_{0}$ . ו- $R_{1}$ מסובב בהזזה מעגלית 8 סיביות שמאלה ואז משמש גם הוא קלט לפונקציה $g$ שמחזירה את $T_{1}$ . התוצאות משולבות יחד באמצעות פונקציית PHT בה מוסיפים שתי מילים מתאימות מהמפתח המורחב לפי $r$ , הפלט הוא הזוג $(F_{0},F_{1})$ ובניסוח פורמלי:

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle T_0=g(R_0)}

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle T_1=g(\mbox{ROL}_8(R_1))}

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle F_0=(T_0+T_1+K_{2r+8}) \mbox{ mod } 2^{32}}

F_{1}=(T_{0}+2T_{1}+K_{2r+9}){\mbox{ mod }}2^{32}

פונקציה g

הפונקציה $g$ מקבלת כפרמטר מילה אחת עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle X} בגודל 32 סיביות, מפצלת אותה לארבעה בתים, כל אחד מהם משמש אינדקס לתיבת ההחלפה המתאימה שמחזירה בית אחר. מייצגים את התוצאות כווקטור באורך 4 מעל השדה $F_{2^{8}}$ ומכפילים במטריצת MDS בגודל 4x4 (ראה תרשים). התוצאה מומרת בחזרה למילה אחת:

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mbox{MDS}=\begin{pmatrix} \mbox{01 EF 5B 5B} \\ \mbox{5B EF EF 01} \\ \mbox{EF 5B 01 EF} \\ \mbox{EF 01 EF 5B} \end{pmatrix}}

x_{i}=\lfloor X/2^{8i}\rfloor {\mbox{ mod }}2^{8}\ \ \ \ \ i=0,...,3

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle y_i=s_i[x_i]\ \ \ \ \ i=0,...,3}

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \begin{pmatrix} z_0 \\ z_1 \\ z_2 \\ z_3 \end{pmatrix}=\begin{pmatrix} \cdot & \cdots & \cdot \\ \vdots & \mbox{MDS} & \vdots \\ \cdot & \cdots & \cdot \end{pmatrix} \cdot \begin{pmatrix} y_0 \\ y_1 \\ y_2 \\ y_3 \end{pmatrix}}

כאשר עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle s_i} היא תיבת החלפה ו- $Z$ הוא התוצאה של $g$ . לצורך המרה בין אלמנטים בשדה $F_{2^{8}}$ לבין בתי הקלט משתמשים בפולינום הפרימיטיבי עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle v(x)=x^8+x^6+x^5+x^3+1} ממעלה 8. האלמנט עיבוד הנוסחה נכשל (שגיאת המרה. השרת ("https://en.wikipedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle a=\textstyle \sum _{i=0}^{7}a_{i}x^{i}} כאשר מקדמיו בינאריים, מתאים לבית $\textstyle \sum _{i=0}^{7}a_{i}2^{i}$ . זהו מיפוי טבעי במובן שפעולות חיבור הן בעצם XOR בלבד.

לצורך יעילות ביישום הן בתוכנה והן בחומרה מיישמים את הכפל במטריצה באמצעות סדרת פעולות XOR ו-Shift תוך שימוש בטכניקה שנקראת LFSR, כדלהלן:

עיבוד הנוסחה נכשל (שגיאת המרה. השרת ("https://en.wikipedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle z_{0}=y_{0}\ \ \oplus \ \ (y_{1}\ \ \oplus \ \ {\mbox{L1}}(y_{1})\ \ \oplus \ \ {\mbox{L2}}(y_{1}))\ \ \oplus \ \ ((y_{2}\ \ \oplus \ \ {\mbox{L2}}(y_{2}))\ \ \oplus \ \ ((y_{3}\ \ \oplus \ \ {\mbox{L2}}(y_{3}))}

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle z_1=(y_0\ \ \oplus \ \ \mbox{L2} (y_0))\ \ \oplus \ \ (y_1\ \ \oplus \ \ \mbox{L1} (y_1)\ \ \oplus \ \ \mbox{L2} (y_1))\ \ \oplus \ \ (y_2\ \ \oplus \ \ \mbox{L1} (y_2) \ \ \oplus \ \ \mbox{L2} (y_2))\ \ \oplus \ \ y_3}

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle z_2=(y_0 \ \ \oplus \ \ \mbox{L1} (y_0)\ \ \oplus \ \ \mbox{L2} (y_0))\ \ \oplus \ \ ((y_1 \ \ \oplus \ \ \mbox{L2} (y_1))\ \ \oplus \ \ y_2 \ \ \oplus \ \ (y_3 \ \ \oplus \ \ \mbox{L1} (y_3)\ \ \oplus \ \ \mbox{L2} (y_3))}

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle z_3=(y_0 \ \ \oplus \ \ \mbox{L1} (y_0)\ \ \oplus \ \ \mbox{L2} (y_1))\ \ \oplus \ \ y_1\ \ \oplus \ \ (y_2\ \ \oplus \ \ \mbox{L1} (y_2)\ \ \oplus \ \ \mbox{L2} (y_2)) \ \ \oplus \ \ ((y_3 \ \ \oplus \ \ \mbox{L2} (y_3))}

והפונקציות L1, L2 הן אוגרי זיזה (LFSR) הראשון מבוסס על הסיבית הראשונה והשני על הסיביות הראשונה והשנייה והן מוגדרות כך:

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mbox{L1}(x) = (x \gg 1)\ \ \oplus \ \ (x \ \ \mbox{AND} \ \ \mbox{0x01} \ \ ? \ \ \mbox{0xB4} \ \ : \ \ 0)}

עיבוד הנוסחה נכשל (שגיאת המרה. השרת ("https://en.wikipedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle {\mbox{L2}}(x)=(x\gg 2)\ \ \oplus \ \ (x\ \ {\mbox{AND}}\ \ {\mbox{0x02}}\ \ ?\ \ {\mbox{0xB4}}\ \ :\ \ 0)\ \ \oplus \ \ (x\ \ {\mbox{AND}}\ \ {\mbox{0x01}}\ \ ?\ \ {\mbox{0x5A}}\ \ :\ \ 0)}

(הסימן עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \gg} מייצג הזזה לימין והסימן AND שנקרא וגם בודק האם הסיבית המתאימה דולקת, 0x02 היא סיבית LSB השנייה). התוצאה היא המרה של ערכי עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle z_i} למילה בגודל 32 סיביות בסדר בתים קטן לפי הנוסחה עיבוד הנוסחה נכשל (שגיאת המרה. השרת ("https://en.wikipedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle \textstyle Z=\sum _{i=0}^{3}z_{i}\cdot 2^{8i}} (במעבד עם סדר בתים קטן, התוצאה מתקבלת במבנה הרצוי ואין צורך בהמרה כלשהי).

הרחבת מפתח

המפתח המורחב מכיל מערך של 40 מילים $K_{0},...,K_{39}$ וארבע תיבות החלפה מהפונקציה $g$ . המפתח כאמור יכול להיות $N=128$ , עיבוד הנוסחה נכשל (שגיאת המרה. השרת ("https://en.wikipedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle N=192} או עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle N=256} סיביות. לצורך הכנת המפתח המורחב יהי עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle k=N/64} , מכינים מהמפתח מערך $M$ בגודל עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 8k} בתים עיבוד הנוסחה נכשל (שגיאת המרה. השרת ("https://en.wikipedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle m_{0},...,m_{8k-1}} (מרפדים באפסים אם נדרש), ממירים ל- $2k$ מילים בגודל 32 סיביות לפי סדר בתים little-endian. ואז ממירים את $M$ לשני וקטורים (זוגי ואי זוגי) כלומר עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle M_e=(M_0,M_2,...,M_{2k-2})} וכן $M_{o}=(M_{1},M_{3},...,M_{2k-1})$ . וקטור נוסף בגודל $k$ מיוצר מהמפתח בקבוצות של 8 סיביות, אותם מפרשים כווקטור מעל $F_{2^{8}}$ ומכפילים במטריצה 4x8 של קוד RS (ריד-סולומון) כמתואר בתרשים להלן. פעולת הכפל במטריצה נראית כך:

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \text{RS}=\begin{pmatrix} \text{01 A4 55 87 5A 58 DB 9E} \\ \text{A4 56 82 F3 1E C6 68 E5} \\ \text{02 A1 FC C1 47 AE 3D 19} \\ \text{A4 55 87 5A 58 DB 9E 03} \end{pmatrix}}

{\begin{pmatrix}s_{i,0}\\s_{i,1}\\s_{i,2}\\s_{i,3}\end{pmatrix}}={\begin{pmatrix}\cdot &\cdots &\cdot \\\vdots &{\mbox{RS}}&\vdots \\\cdot &\cdots &\cdot \end{pmatrix}}\cdot {\begin{pmatrix}m_{8i}\\m_{8i+1}\\m_{8i+2}\\m_{8i+3}\\m_{8i+4}\\m_{8i+5}\\m_{8i+6}\\m_{8i+7}\end{pmatrix}}

ואז מחשבים עבור עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle i=0,...,k-1} בסדר הפוך עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle S = (S_{k-1},S_{k-2},...,S_0)} :

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle S_i=\sum_{j=0}^3 s_{i,j}\cdot 2^{8j}}

להכפלה במטריצה בשיטת ריד-סולומון, משתמשים בפולינום פרימיטיבי $w(x)=x^{8}+x^{6}+x^{3}+x^{2}+1$ .

שלושת הווקטורים עיבוד הנוסחה נכשל (שגיאת המרה. השרת ("https://en.wikipedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle M_{e},M_{o},S} הם הבסיס לתהליך הרחבת המפתח.

פונקציה h

הפונקציה המשמשת להרחבת המפתח מקבלת פרמטר עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle X} בגודל 32 סיביות ורשימה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle L=(L_0,...,L_{k-1})} של מילות 32 סיביות באורך $k$ ומפיקה מילה אחת. הפונקציה פועלת באופן איטרטיבי $k$ שלבים, בכל שלב 4 בתים עוברים בתיבות החלפה קבועות ומחוברים ב-XOR עם בתים מהרשימה $L$ ולסיום מועברים שוב בתיבות ההחלפה ומוכפלים במטריצת MDS. כדלהלן: תחילה מפצלים לבתים כאשר עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle i=0,...,k-1} ו-עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle j=0,...,3} :

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle l_{u,j}=\left \lfloor L_i/2^{8j} \right \rfloor \mbox{ mod }2^8}

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle x_j=\left \lfloor X/2^{8j} \right \rfloor \mbox{ mod }2^8}

בשלב החלפה ו-XOR תחילה מציבים עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle y_{k,j}=x_j} כאשר עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle j=0,...,3} ואז מחשבים לפי ערך $k$ :

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle k = 4}	עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle k \ge 3}	In all cases
$y_{3,0}=q_{1}[y_{4,0}]\oplus l_{3,0}$	$y_{2,0}=q_{1}[y_{3,0}]\oplus l_{2,0}$	עיבוד הנוסחה נכשל (שגיאת המרה. השרת ("https://en.wikipedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle y_{0}=q_{1}[q_{0}[q_{0}[y_{2,0}]\oplus l_{1,0}]\oplus l_{0,0}]}
$y_{3,1}=q_{0}[y_{4,1}]\oplus l_{3,1}$	$y_{2,1}=q_{1}[y_{3,1}]\oplus l_{2,1}$	$y_{1}=q_{0}[q_{0}[q_{1}[y_{2,1}]\oplus l_{1,1}]\oplus l_{0,1}]$
עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle y_{3,2} = q_0[y_{4,2}] \oplus l_{3,2}}	עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle y_{2,2} = q_0[y_{3,2}] \oplus l_{2,2}}	$y_{2}=q_{1}[q_{1}[q_{0}[y_{2,2}]\oplus l_{1,2}]\oplus l_{0,2}]$
עיבוד הנוסחה נכשל (שגיאת המרה. השרת ("https://en.wikipedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle y_{3,3}=q_{1}[y_{4,3}]\oplus l_{3,3}}	עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle y_{2,3} = q_0[y_{3,3}] \oplus l_{2,3}}	עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle y_3 = q_0[q_1[q_1[y_{2,3}] \oplus l_{1,3}] \oplus l_{0,3}]}

כאשר עיבוד הנוסחה נכשל (שגיאת המרה. השרת ("https://en.wikipedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle q_{0},q_{1}} הן תמורות קבועות של ערכים בגודל 8 סיביות המוגדרות להלן. הווקטור $y_{i}$ מוכפל במטריצת MDS כמו בפונקציה $g$ לעיל:

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \begin{pmatrix} z_0 \\ z_1 \\ z_2 \\ z_3 \end{pmatrix}=\begin{pmatrix} \cdot & \cdots & \cdot \\ \vdots & \mbox{MDS} & \vdots \\ \cdot & \cdots & \cdot \end{pmatrix} \cdot \begin{pmatrix} y_0 \\ y_1 \\ y_2 \\ y_3 \end{pmatrix}}

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle Z=\sum_{i=0}^3 z_i \cdot 2^{8i}}

תיבות החלפה S-box

כאמור תיבות ההחלפה תלויות במפתח, ליתר דיוק בוקטור עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle S} שהוכן מהמפתח לעיל. דהיינו ארבע התיבות מחושבות מתוך עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle x_i,y_i} עבור $i=0,...,3$ בפונקציה $h$ כאשר הרשימה $L$ היא עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle S} בתמציתיות: $g(X)=h(X,S)$ .

המפתח המורחב K

עם השלמת הגדרת הפונקציה $h$ , אפשר להשלים את תהליך הרחבת המפתח כדלהלן:

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \rho=2^{24}+2^{16}+2^8+1}

A_{i}=h(2i\rho ,M_{e})

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle B_i=\mbox{ROL}(h((2i+1)\rho,M_o),8)}

K_{2i}=(A_{i}+B_{i}){\mbox{ mod }}2^{32}

עיבוד הנוסחה נכשל (שגיאת המרה. השרת ("https://en.wikipedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle K_{2i+1}={\mbox{ROL}}((A_{i}+2B_{i}){\mbox{ mod }}2^{32},9)}

הקבוע עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \rho} משמש כאן להכפלת בתים, התכונה שלו היא שהמילה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle i\rho } מורכבת מארבעה בתים שווים בערכם ל-עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle i} . שים לב שנעשה שימוש בהזזה מעגלית, בוקטורים עיבוד הנוסחה נכשל (שגיאת המרה. השרת ("https://en.wikipedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle M_{e},M_{o}} ובפונקציית PHT. התמורות הקבועות $q_{0}$ ו-עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle q_1} מחושבות מתוך 4 תמורות שונות, עבור קלט עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle x} מחשבים את הפלט $y$ על ידי:

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_0,b_0=\left \lfloor x/16 \right \rfloor, x\mbox{ mod }16}

a_{1}=a_{0}\oplus b_{0}

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle b_1=a_0 \oplus \mbox{ROR}_4(b_0,1) \oplus 8a_0 \mbox{ mod }16}

a_{2},b_{2}=t_{0}[a_{1}],t_{1}[b_{1}]

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_3=a_2 \oplus b_2}

b_{3}=a_{2}\oplus {\mbox{ROR}}_{4}(b_{2},1)\oplus 8a_{2}{\mbox{ mod }}16

a_{4},b_{4}=t_{2}[a_{3}],t_{3}[b_{3}]

y=16b_{4}+a_{4}

תחילה מפצלים את הבית לשני ניבלים, שעוברים שלב ערבוב עם פונקציה חד-חד-ערכית ועל, כל ניבל עובר בנוסף בתיבת החלפה של 4 סיביות קבועה משלו ואז מאחדים את הניבלים. תיבות ההחלפה 4-סיביות הן:

$q_{0}$	עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle q_1}
עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle t_0 = [ \mbox{817D6F320B59ECA4} ]}	עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle t_0 = [ \mbox{28BDF76E31940AC5} ] }
$t_{1}=[{\mbox{ECB81235F4A6709D}}]$	$t_{1}=[{\mbox{1E2B4C376DA5F908}}]$
עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle t_2 = [ \mbox{BA5E6D90C8F32471} ]}	עיבוד הנוסחה נכשל (שגיאת המרה. השרת ("https://en.wikipedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle t_{2}=[{\mbox{4C75169A0ED82B3F}}]}
עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle t_3 = [ \mbox{D7F4126E9B3085CA} ]}	$t_{3}=[{\mbox{B951C3DE647F208A}}]$

פענוח

צופן Twofish משתמש בתהליך הכנה מעט שונה עבור פענוח. השוני הוא בסדר ההפוך של המפתח המורחב $K$ . כמובן שבגרסאות הממוטבות ביישום האלגוריתם בפועל, נמנעים בדרך כלל מפעולות אריתמטיות מוסבכות, אותם מחליפים בטבלאות החלפה פשוטות בהם הערכים קודדו מראש בהתאם. ובמקרה של יישום בחומרה מוגבלת כמו כרטיס חכם, מפרקים פעולות לפקודות בסיסיות ביותר כמו Shift ו-XOR, לעיתים על חשבון יעילות.

ראו גם

קישורים חיצוניים

ברוס שנייר, Twofish, Schneier on Security

הערך באדיבות ויקיפדיה העברית, קרדיט,
רישיון cc-by-sa 3.0

This article is issued from Hamichlol. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.