שיטות אנליטיות לחישוב אינטגרלים מסוימים

לחלק מהאינטגרלים לא ניתן מצד אחד לקבל פתרון עבור האינטגרל הלא-מסוים אולם מהצד השני ניתן לקבל פתרונות אנליטיים (כלומר כאלו שאינם מצריכים אנליזה נומרית) עבור גבולות מסוימים של אינטגרל מסוים.

להלן רשימה חלקית של שיטות לביצוע תהליך האינטגרציה כזה:

זוגיות ואי-זוגיות

כאשר יש פונקציה אי-זוגית ביחס לנקודה ${\displaystyle a}$ , כלומר מתקיים עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f(a+x)=-f(a-x)} והאינטגרל סימטרי סביב הנקודה ${\displaystyle a}$ , כלומר הגבולות הם מהצורה ${\displaystyle (a-b,a+b)}$ אזי האינטגרל הוא אפס;

למשל: עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \int\limits_\pi^{3\pi}\sin(x)dx=0}

פונקציה זוגית סביב הנקודה ${\displaystyle a}$ ניתנת לחישוב רק בחצי מהתחום (מעל או מתחת לנקודה ${\displaystyle a}$) תוך הכפלה בשניים. למשל:

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \int\limits_{-8}^8|x|dx=2\int\limits_0^8x\,dx=2\left[\frac{x^2}{2}\right]_0^8=\bigl[x^2\bigr]_0^8 =(64-0)=64}

חישוב במסלול סגור במישור המרוכב

כאשר מבצעים המשכה אנליטית של פונקציה ממשית למישור המרוכב, ניתן להשלים את מסלול האינטגרציה במישור המרוכב כך שיווצר מסלול סגור שניתן לחשב אותו באמצעות משפטים המתאימים לאינטגרל קווי במישור המרוכב כמו משפט האינטגרל של קושי, נוסחת האינטגרל של קושי, ובעיקר משפט השאריות.

השיטה מתבססת על יצירת מסלול סגור ${\displaystyle C}$ המכיל את הקטע עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (a,b)} המופיע באינטגרל המקורי (אותו נסמן עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle I} ), וחישוב האינטגרל במסלול ${\displaystyle C}$ (אותו נסמן עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle I_C} ) ובקטעים האחרים המופיעים במסלול.

כך מגיעים למשוואה מהצורה: עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f(I)=I_C} כאשר עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f} היא פונקציה הפיכה בתחום המתאים ל-עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle I} (בפרט אינטגרל של פונקציה ממשית הוא תמיד ממשי).

דוגמה

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \begin{align} \int\limits_0^{2\pi}\frac1{1+\sin(x)}dx&= \\ &=\left[\begin{matrix}\sin(x)=\dfrac{z-z^{-1}}{2}\\dx=\dfrac{dz}{iz}\end{matrix}\right] \\ &=\oint\limits_{|z|=1}\frac{\frac{dz}{iz}}{1+\frac{z-z^{-1}}{2}}=-\frac{i}{2}\oint\limits_{|z|=1}\frac{dz}{2z+z^2-1} \\ &=-\frac{i}{2}\oint\limits_{|z|=1}\frac{\frac{dz}{z+1+\sqrt2}}{z+1-\sqrt2}=-\frac{i}{2}\cdot2\pi i\left[\frac1{z+1+\sqrt2}\right]_{z=-1+\sqrt{2}} \\ &=\frac{\pi}{-1+\sqrt2+1+\sqrt2}=\frac{\pi}{2\sqrt2} \end{align}}

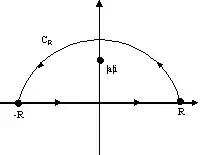
את האינטגרל עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \begin{align}\int\limits_{-\infty}^\infty\frac{\exp\left(\frac{pxi}{\hbar}\right)}{x^2+a^2}dx\end{align}} , כאשר ${\displaystyle \hbar >0,p,a}$ , ניתן לחשב על ידי סגירת המסלול הסגור המצויר בצד שמאל והשאפת עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle R} לאינסוף.

תחילה נפתח אותו לצורה נוחה יותר:

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \begin{align}\int\limits_{-\infty}^\infty\frac{\exp\left(\frac{pxi}{\hbar}\right)}{x^2+a^2}dx=\int\limits_{-R}^R\frac{\exp\left(\frac{pzi}{\hbar}\right)}{(z+|a|i)(z-|a|i)}dz\end{align}}

על פי נוסחת אינטגרל קושי על המסלול הסגור מקבלים כי:

עיבוד הנוסחה נכשל (שגיאת המרה. השרת ("https://en.wikipedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle {\begin{aligned}\int \limits _{-R}^{R}{\frac {\exp \left({\frac {pzi}{\hbar }}\right)}{(z+|a|i)(z-|a|i)}}dz&+\int \limits _{C_{R}}{\frac {\exp \left({\frac {pzi}{\hbar }}\right)}{(z+|a|i)(z-|a|i)}}dz\\&=\oint \limits _{C}{\frac {\exp \left({\frac {pzi}{\hbar }}\right)}{(z+|a|i)(z-|a|i)}}dz\\&=2\pi i\left.{\frac {\exp \left({\frac {pzi}{\hbar }}\right)}{z+|a|i}}\right|_{z=|a|i}\\&=2\pi i{\frac {\exp \left({\frac {ip|a|i}{\hbar }}\right)}{|a|i+|a|i}}={\frac {\pi }{|a|}}\exp \left(-{\frac {p|a|}{\hbar }}\right)\end{aligned}}}

על פי למת ז'ורדן מקבלים כי:

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \begin{align}\lim_{R\to0}\int\limits_{C_R}\frac{\exp\left(\frac{pzi}{\hbar}\right)}{(z+|a|i)(z-|a|i)}dz=0\end{align}}

ועל ידי הצבה מקבלים:

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \begin{align} \int\limits_{-\infty }^\infty\frac{\exp\left(\frac{pzi}{\hbar}\right)}{(z+|a|i)(z-|a|i)}dz&= \\ &=\int\limits_{-\infty}^\infty\frac{\exp\left(\frac{pzi}{\hbar}\right)}{(z+|a|i)(z-|a|i)}dz+0 \\ &=\lim_{R\to\infty}\int\limits_{-R}^R\frac{\exp\left(\frac{pzi}{\hbar}\right)}{(z+|a|i)(z-|a|i)}dz+\lim_{R\to\infty}\int\limits_{C_R}\frac{\exp\left(\frac{pzi}{\hbar}\right)}{(z+|a|i)(z-|a|i)}dz \\ &=\lim_{R\to\infty}\left(\int\limits_{-R}^R\frac{\exp\left(\frac{pzi}{\hbar}\right)}{(z+|a|i)(z-|a|i)}dz+\int\limits_{C_R}\frac{\exp\left(\frac{pzi}{\hbar}\right)}{(z+|a|i)(z-|a|i)}dz\right) \\ &=\lim_{R\to\infty}\oint\limits_C\frac{\exp\left(\frac{pzi}{\hbar}\right)}{(z+|a|i)(z-|a|i)}dz=\lim_{R\to\infty}\frac{\pi}{|a|}\exp\left(-\frac{p|a|}{\hbar}\right) \\ &=\frac{\pi}{|a|}\exp\left(-\frac{p|a|}{\hbar}\right) \end{align}}

ובסה"כ מתקיים:

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \begin{align} \int\limits_{-\infty}^\infty\frac{\exp\left(\frac{pxi}{\hbar}\right)}{x^2+a^2}dx=\frac{\pi}{|a|}\exp\left(-\frac{p|a|}{\hbar}\right) \end{align}}

מעבר למערכת קואורדינטות אחרת

כאשר לאינטגרל יש סימטריה כלשהי, ניתן לעבור למערכת קואורדינטות אחרת שבה הוא מופיע בצורה פשוטה יותר. מעבר כזה מהווה למעשה מקרה פרטי של שיטת ההצבה.

דוגמה – חישוב שטח עיגול (בעל רדיוס עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle R} ):
עוברים ממערכת צירים קרטזית למערכת קואורדינטות קוטביות ומקבלים אינטגרל פשוט הרבה יותר:

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \begin{align}S(R)=\int\limits_0^R dy\!\!\int\limits_0^{\sqrt{R^2-y^2}}\!\!\!\!\!\!dx=\int\limits_0^Rr\,dr\int\limits_0^{2\pi}d\phi=\pi R^2\end{align}}

דוגמה נוספת:

חישוב האינטגרל הבא: ${\displaystyle {\begin{aligned}I=\int \limits _{-\infty }^{\infty }e^{-x^{2}}dx\end{aligned}}}$

$${\displaystyle {\begin{aligned}I^{2}=\int \limits _{-\infty }^{\infty }e^{-x^{2}}dx\int \limits _{-\infty }^{\infty }e^{-y^{2}}dy=\int \limits _{-\infty }^{\infty }\int \limits _{-\infty }^{\infty }e^{-(x^{2}+y^{2})}dx\,dy=\int \limits _{0}^{2\pi }\int \limits _{0}^{\infty }re^{-r^{2}}dr\,d\phi =\pi \end{aligned}}}$$

שימוש בהתמרות

יש מקרים בהם ניתן להציג את האינטגרל המסוים בעזרת התמרה מסוימת (למשל התמרת פורייה) ולהשתמש בתכונות שלה.

לדוגמה: נחשב את עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \begin{align}\int\limits_0^\infty\frac{\sin(x)}{x}dx\end{align}} .

נגדיר פונקציה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f(t)=\frac1{\sin(t)}-\frac1t} . קל לבדוק כי עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f} בעלת נקודת אי-רציפות סליקה בנקודה 0, ולכן נוכל להתייחס אל עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f} כאל פונקציה הרציפה בקטע ${\displaystyle \left[-{\tfrac {\pi }{2}},{\tfrac {\pi }{2}}\right]}$ .

לכן עיבוד הנוסחה נכשל (שגיאת המרה. השרת ("https://en.wikipedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle g=f\left({\tfrac {t}{2}}\right)} רציפה בקטע ${\displaystyle [-\pi ,\pi ]}$ .

מהלמה של רימן-לבג אפשר לראות שמתקיים:

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \begin{align}\lim_{n\to\pm\infty}\hat g(n)=\frac1{2\pi}\lim_{n\to\pm\infty}\int\limits_{-\pi}^\pi g(t)e^{-tni}dt=0\end{align}}

כאשר: עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \begin{align}\hat g(n)=\frac1{2\pi}\int\limits_{-\pi}^\pi g(t)e^{-tni}dt\end{align}} מקדמי הפורייה של עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle g} .

לכן:

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \frac1{2\pi}\lim_{n\to\pm\infty}\int\limits_{-\pi}^\pi f\left(\tfrac{t}{2}\right)e^{-tni}dt=\frac1{2\pi}\lim\limits_{n\to\pm\infty}\int\limits_{-\pi}^\pi\left(\frac1{\sin\left(\frac{t}{2}\right)}-\frac1{\frac{t}{2}}\right)e^{-tni}dt=0}

בפרט, גם:

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \begin{align}\frac1{2\pi}\lim_{n\to\pm\infty}\int\limits_{-\pi}^\pi\left(\frac1{\sin\left(\frac{t}{2}\right)}-\frac1{\frac{t}{2}}\right)e^{tni}dt=0\end{align}}

ולכן:

עיבוד הנוסחה נכשל (שגיאת המרה. השרת ("https://en.wikipedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle {\frac {1}{2\pi }}\lim _{n\to \infty }\int \limits _{-\pi }^{\pi }\left({\frac {1}{\sin \left({\frac {t}{2}}\right)}}-{\frac {1}{\frac {t}{2}}}\right)\sin {\bigl (}(n+{\tfrac {1}{2}})t{\bigr )}dt=0}

כי מנוסחת אוילר: עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \sin(t)=\frac{e^{ti}-e^{-ti}}{2i}}

כלומר:

$${\displaystyle {\frac {1}{2\pi }}\lim _{n\to \infty }\int \limits _{-\pi }^{\pi }\left({\frac {\sin \left((n+{\tfrac {1}{2}})t\right)}{\sin \left({\tfrac {t}{2}}\right)}}-{\frac {\sin \left((n+{\tfrac {1}{2}})t\right)}{\tfrac {t}{2}}}\right)dt=0}$$

נחלק לשני אינטגרלים, ונקבל:

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \lim_{n\to\infty}\left(\int\limits_{-\pi}^\pi\frac1{2\pi}\cdot\frac{\sin\left((n+\tfrac12)t\right)}{\sin\left(\tfrac{t}{2}\right)}dt-\int\limits_{-\pi}^\pi\frac1{2\pi}\cdot\frac{\sin\left((n+\tfrac12)t\right)}{\tfrac{t}{2}}dt\right)=0}

האינטגרל השמאלי הוא אינטגרל של גרעין דיריכלה, ולכן שווה 1 לכל עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle n} טבעי.

$${\displaystyle \lim _{n\to \infty }\left(1-\int \limits _{-\pi }^{\pi }{\frac {1}{2\pi }}\cdot {\frac {\sin \left((n+{\tfrac {1}{2}})t\right)}{\tfrac {t}{2}}}dt\right)=0}$$

האינטגרל שנותר הוא של פונקציה זוגית, ולכן ניתן להחליף את התחום ב-${\displaystyle [0,\pi ]}$ ולהכפיל ב-2:

עיבוד הנוסחה נכשל (שגיאת המרה. השרת ("https://en.wikipedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle \lim _{n\to \infty }\left(1-\int \limits _{0}^{\pi }{\frac {1}{\pi }}\cdot {\frac {\sin \left((n+{\tfrac {1}{2}})t\right)}{\tfrac {t}{2}}}dt\right)=0}

כלומר:

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \begin{align}\lim_{n\to\infty}\int\limits_0^\pi\frac{\sin\left((n+\frac12)t\right)}{t}dt=\frac{\pi}{2}\end{align}}

על ידי הצבה ${\displaystyle s=\left(n+{\tfrac {1}{2}}\right)t}$ נקבל:

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \lim_{n\to\infty}\int\limits_0^{\left(n+\tfrac12\right)\pi}\frac{\sin(s)}{s}ds=\frac{\pi}{2}}

ומכיוון שהאינטגרל מתכנס (ממבחן דיריכלה), מתקיים:

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \begin{align}\int\limits_0^\infty\frac{\sin(s)}{s}ds=\frac{\pi}{2}\end{align}}

ראו גם

• שיטות אינטגרציה
• שיטות למציאת אינטגרלים לא מסוימים
• שיטות נומריות לחישוב אינטגרלים מסוימים

קישורים חיצוניים

• The Wolfram Integrator – חישוב אינטגרלים לא מסוימים