חבורה ציקלית

בתורת החבורות, חבורה ציקלית היא חבורה הנוצרת על ידי איבר אחד. כלומר כל אחד מאברי החבורה הוא חזקה של האיבר היוצר. כל חבורה כזו היא אבלית לפי כללי חזקות וחילופיות פעולת החיבור.

חבורות ציקליות הן הדוגמה הפשוטה ביותר לחבורה, ולפי משפט המיון לחבורות אבליות נוצרות סופית, אפשר להרכיב מהן (באמצעות מכפלה ישרה) את החבורות האבליות הנוצרות סופית. אם מרשים הרכבה מסובכת יותר, אפשר לבנות מן החבורות הציקליות את כל החבורות הפתירות.

חבורות ציקליות הן דוגמה למושג הכללי יותר, מודול ציקלי.

הגדרה, יחידות וסימון

באופן פורמלי, חבורה ציקלית היא חבורה ${\displaystyle \ G}$ שבה קיים איבר עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ g\in G} שהחזקות שלו מרכיבות את החבורה כולה. לאיבר כזה קוראים יוצר של החבורה. כאשר משתמשים בכתיב כפלי, מקובל לסמן את החבורה הציקלית הנוצרת על ידי איבר עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ g} בסימון עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ \langle g \rangle} .

כל שתי חבורות ציקליות בעלות אותו סדר הן איזומורפיות זו לזו, ולכן מוצדק לדבר על החבורה הציקלית מסדר n, בה"א הידיעה. כאשר רוצים להדגיש את סדר החבורה, מקובל לסמן את החבורה הציקלית הנוצרת על ידי איבר עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ g} מסדר n, כ־${\displaystyle \ \langle g|g^{n}=1\rangle }$ ואפילו ${\displaystyle \ \langle g|g^{n}\rangle }$ (ראו חבורה מוצגת סופית).

החבורה האינסופית ${\displaystyle \ \mathbb {Z} }$ הכוללת את כל המספרים השלמים, ביחס לפעולת החיבור, היא ציקלית. כל איבר שלה מתקבל מסיכום היוצר עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ 1} לעצמו, מספר סופי של פעמים. חבורת המנה ${\displaystyle \ \mathbb {Z} /n\mathbb {Z} }$, המורכבת מן המספרים עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ \{0,1,2,\dots,n-1\}} עם פעולת החיבור מודולו המספר הטבעי ${\displaystyle \ n}$, היא חבורה ציקלית מסדר ${\displaystyle \ n}$ , כאשר גם כאן עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ 1} הוא יוצר של החבורה. בהתאם לאיזומורפיזם של חבורות ציקליות מאותו סדר, נהוג להשתמש בחבורות אלו לייצוג כל החבורות הציקליות, כך שחבורה ציקלית מסדר ${\displaystyle \ n}$ מיוצגת על ידי הסימון עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ \mathbb{Z}_n} (כלומר עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ \mathbb{Z}_n = \mathbb{Z}/n\mathbb{Z}} ^[1]), וכל חבורה ציקלית אינסופית מיוצגת על ידי הסימון ${\displaystyle \ \mathbb {Z} }$ .

בכל חבורה, תת־החבורה הנוצרת על ידי איבר אחד עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ g} (ומורכבת, על־פי ההגדרה, מכל החזקות ${\displaystyle \ \{g^{k}:k\in \mathbb {Z} \}}$), היא חבורה ציקלית.

איברים

היוצר של חבורה ציקלית כמעט לעולם אינו יחיד. החבורה הציקלית האינסופית ${\displaystyle \ \mathbb {Z} }$ נוצרת על ידי עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ 1} או על ידי עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ -1} . לחבורה ציקלית עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ \langle g \rangle} מסדר ${\displaystyle \ n}$ יש עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ \varphi(n)} יוצרים (כאשר עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ \varphi} היא פונקציית אוילר), שהם בדיוק החזקות עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ g^k} עבורן ${\displaystyle \ k}$ זר ל-${\displaystyle \ n}$ .

באופן כללי יותר, ההסדר של איבר עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ g^k} הוא ${\displaystyle \ {\frac {n}{\gcd(n,k)}}}$, כאשר עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ \gcd(n,k)} הוא המחלק המשותף המקסימלי של עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ n,k} .

חבורת האוטומורפיזמים

מכיוון שאוטומורפיזם מוכרח להעביר יוצר של החבורה ליוצר אחר, יש לחבורה הציקלית מסדר ${\displaystyle \ n}$ בדיוק עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ \varphi(n)} אוטומורפיזמים, וניתן להבחין שחבורת האוטומורפיזמים שלה איזומורפית לחבורת אוילר ${\displaystyle \ U_{n}}$ .

גאוס מצא שחבורת אוילר ${\displaystyle \ U_{n}}$ היא ציקלית בדיוק כאשר ${\displaystyle \ n}$ שווה ל־2, 4, חזקה של ראשוני אי־זוגי, או פעמיים חזקה של ראשוני אי־זוגי.

פירוק לגורמים

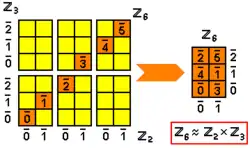
המכפלה הישרה של שתי חבורות ציקליות עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ \mathbb{Z}/n\mathbb{Z} \times \mathbb{Z}/m\mathbb{Z}} היא חבורה ציקלית, אם ורק אם n ו- m זרים. במקרה זה, כמובן, היא איזומורפית ל־עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ \mathbb{Z}/mn\mathbb{Z}} . מן המשפט היסודי של האריתמטיקה נובע שאפשר לפרק כל חבורה ציקלית למכפלה ישרה של חבורות ציקליות שכל אחת מהן מסדר חזקה של ראשוני. למשל

עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ \mathbb{Z}/720\mathbb{Z} \cong \mathbb{Z}/16\mathbb{Z}\times \mathbb{Z}/9\mathbb{Z} \times \mathbb{Z}/5\mathbb{Z}}

הערות שוליים