חוג השלמים של גאוס

מספרים שלמים של גאוס כנקודות סריג במישור המרוכב

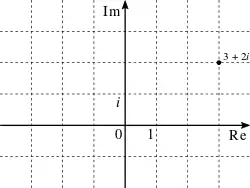
חוג השלמים של גאוס הוא אוסף המספרים ${\displaystyle \mathbb {Z} [i]=\{a+bi:a,b\in \mathbb {Z} \}}$ כאשר ${\displaystyle i}$ היחידה המרוכבת (${\displaystyle i^{2}=-1}$), היינו, מספרים מרוכבים בעלי קואורדינטות שלמות. אוסף זה, שהוא חוג המספרים השלמים בשדה ${\displaystyle \mathbb {Q} [i]}$ , הוא חוג אוקלידי, ולכן יש בו פירוק יחיד לגורמים.

הנורמה מוגדרת על החוג הזה לפי הנוסחה ${\displaystyle N(a+bi)=(a+bi)(a-bi)=a^{2}+b^{2}}$ , זוהי פונקציה כפלית, השווה לריבוע הערך המוחלט של מספרים מרוכבים. חוג השלמים של גאוס הוא אוקלידי ביחס לנורמה: לכל ${\displaystyle x}$ ולכל ${\displaystyle y\neq 0}$ קיים ${\displaystyle r}$ עבורו ${\displaystyle N(x-ry)<N(y)}$ . בזכות האוקלידיות אפשר לחשב מחלק משותף מקסימלי באמצעות אלגוריתם אוקלידס, ולכל מספר יש פירוק יחיד לגורמים ראשוניים.

הראשוניים של גאוס

כמו בכל תחום שלמות, איבר אי-פריק הוא איבר ${\displaystyle x}$ שאי-אפשר לפרק בלי שאחד הגורמים יהיה הפיך. מכיוון שזהו תחום פריקות יחידה, כל איבר אי-פריק עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \pi} הוא גם ראשוני (הוא אינו מחלק מכפלה בלי לחלק את אחד הגורמים שלה).

לא כל מספר ראשוני במובן הרגיל של המלה נשאר ראשוני גם בחוג השלמים של גאוס. למשל, עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 5=(2+i)(2-i)} , ולכן 5 פריק ואינו ראשוני. עם זאת, אם עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \pi} ראשוני אז הנורמה שלו עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \pi\bar\pi} היא או מספר ראשוני, במובן הרגיל של המלה, או ריבוע של מספר כזה (אכן, עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \pi} מחלק את אחד הגורמים הראשוניים של המספר השלם עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \pi\bar\pi} , נאמר עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \pi|p} , ואז גם ${\displaystyle {\bar {\pi }}|p}$ ולכן עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \pi\bar\pi|p^2} ). מכאן מתקבלת חלוקה של הראשוניים, עד כדי כפל באיבר הפיך, לשלוש קבוצות:

• אלו המחלקים את 2: זהו הראשוני עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 1+i} (הגורם השני עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 1-i} נוצר מהכפלת הראשון באיבר הפיך עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle -i} ).
• אלו המחלקים ראשוני רציונלי ${\displaystyle p}$ השקול ל-1 מודולו 4: לפי משפט של פרמה, כל ראשוני כזה הוא סכום של שני ריבועים ${\displaystyle p=a^{2}+b^{2}}$ , ואז עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a\pm bi} הם שני הגורמים הראשוניים של ${\displaystyle p}$ .
• הראשוניים הרציונליים השקולים ל-3 מודולו 4.

תורת המספרים האלגברית לומדת בין השאר את הפירוק של אידאלים ראשוניים של ${\displaystyle \mathbb {Z} }$ בחוג הגדול יותר ${\displaystyle \mathbb {Z} [i]}$ . בהתאמה לשלוש הקבוצות של ראשוניים שהוזכרו לעיל, 2 הוא ראשוני מסועף, עם ${\displaystyle e=2}$ (ראו e, f ו-g); לראשוניים השקולים ל-1 מודולו 4 יש ${\displaystyle g=2}$ ; ולראשוניים הנותרים יש עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f=2} . למשוואה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle x^2+1\equiv0\pmod p} יש פתרון אם ורק אם ${\displaystyle f=1}$ , כלומר בשני המקרים הראשונים.

ראו גם

• חוג השלמים של אייזנשטיין

מערכות מספרים
מספרים	המספרים הטבעיים ${\displaystyle \mathbb {N} }$ (מערכת פאנו) • חוג המספרים השלמים ${\displaystyle \mathbb {Z} }$ (מספרים חיוביים ושליליים, מספר שלם) • שדה המספרים הרציונליים ${\displaystyle \mathbb {Q} }$ (מספר רציונלי, מספר אי-רציונלי) • שדה המספרים הממשיים ${\displaystyle \mathbb {R} }$ (הישר הממשי, מספר ממשי) • שדה המספרים המרוכבים עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mathbb{C}} (המישור המרוכב, מספר מרוכב, מספר מדומה)
הרחבות של חוג המספרים השלמים	חוג השלמים של גאוס ${\displaystyle \ \mathbb {Z} [i]}$ • חוג השלמים האלגבריים ${\displaystyle \ {\overline {\mathbb {Z} }}}$ • חוג השלמים של אייזנשטיין עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ \mathbb{Z}[\omega]}
הרחבות של שדה המספרים הרציונליים	שדה מספרים • שדה המספרים הניתנים לבנייה • שדה המספרים האלגבריים עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ \overline{\mathbb{Q}}} (מספר אלגברי, מספר טרנסצנדנטי) • שדה המספרים ה-p-אדיים ${\displaystyle \mathbb {Q} _{p}}$ (מספר p-אדי) • שדה ציקלוטומי
מעבר למרוכבים	אלגברת הקווטרניונים של המילטון ${\displaystyle \ {\mathbb {H} }}$ • אוקטוניונים ${\displaystyle \ {\mathbb {O} }}$ • אלגברות קיילי-דיקסון