מרחב המסרק

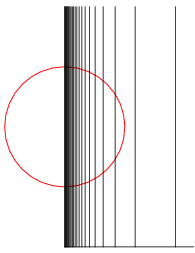
מרחב המסרק, המוגדר על ידי איחוד של ציר X עם קווים המקבילים לציר Y במרחק ${\displaystyle \,1/n}$ הנו קשיר מסילתית, אך אינו קשיר מקומית סביב הנקודה המסומנת

בטופולוגיה, מרחב המסרק הוא תת־מרחב של המרחב הטופולוגי ${\displaystyle \mathbb {R} ^{2}}$ , אשר דומה למסרק.

למרחב המסרק תכונות טופולוגיות מעניינות, והוא מהווה דוגמה נגדית נוחה במקרים רבים.

משפט היינה-בורל, ומשפטים חזקים נוספים, מאפשרים לתאר את הקבוצות הקומפקטיות במרחב האוקלידי. אפילו במקרה זה, המבנה של קבוצות קשירות מורכב יותר. למשל, כל מרחב האוסדורף קומפקטי הוא קומפקטי מקומית, ועם זאת, מרחב קשיר אינו חייב להיות קשיר מקומית, אפילו אם מדובר על תת־מרחב של המרחב האוקלידי (ראו מרחב המסרק באיור משמאל).

הגדרה פורמלית

נתבונן ב־${\displaystyle \mathbb {R} ^{2}}$ עם הטופולוגיה הסטנדרטית. תהי ${\displaystyle K}$ הקבוצה ${\displaystyle \{0\}\cup \{1/n\mid n\in \mathbb {N} \}}$ . קבוצת המסרק ${\displaystyle C}$ מוגדרת:

${\displaystyle C=(K\times [0,1])\cup ([0,1]\times \{0\})}$

הקבוצה הראשונה באיחוד היא ה"שיניים" של המסרק, ואילו הקבוצה השנייה היא ה"ידית" שלו. הקבוצה ${\displaystyle C}$ עם הטופולוגיה המושרית היא מרחב המסרק.

קשירות

מרחב המסרק הוא דוגמה למרחב קשיר שאינו מרחב קשיר מקומית.

ראו גם

• עקומת הסינוס של הטופולוגים