התפלגות ריילי

התפלגות ריילי
פונקציית צפיפות ההסתברות
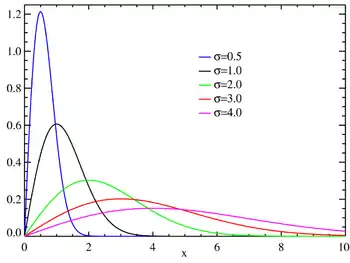פונקציית ההסתברות המצטברת
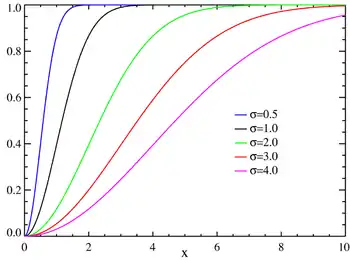מאפיינים
פרמטרים	${\displaystyle \ \sigma }$
תומך	עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ [0,\infty)}
פונקציית צפיפות הסתברות (pdf)	עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ \frac{x}{\sigma^2}\exp(-\frac{x^2}{2\sigma^2})}
פונקציית ההסתברות המצטברת (cdf)	עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ 1-\exp(-\frac{x^2}{2\sigma^2})}
תוחלת	עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \sqrt{\frac{\pi}{2}}\cdot \sigma}
סטיית תקן	${\displaystyle \ {\sqrt {\frac {4-\pi }{2}}}\sigma }$
חציון	${\displaystyle \sigma {\sqrt {\ln(4)}}\,}$
ערך שכיח	${\displaystyle \sigma \,}$
שונות	${\displaystyle {\frac {4-\pi }{2}}\sigma ^{2}}$
אנטרופיה	${\displaystyle 1+\ln \left({\frac {1}{{\sqrt {2}}\sigma ^{3}}}\right)+{\frac {\gamma }{2}}}$
פונקציה יוצרת מומנטים (mgf)	${\displaystyle M_{X}(t)=\exp \left(\mu \,t+{\frac {\sigma ^{2}t^{2}}{2}}\right)}$
צידוד	עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \frac{2\sqrt{\pi}(\pi - 3)}{(4-\pi)^{3/2}}}
גבנוניות	${\displaystyle -{\frac {6\pi ^{2}-24\pi +16}{(4-\pi )^{2}}}}$

בהסתברות ובסטטיסטיקה, התפלגות ריילי היא התפלגות רציפה, המתקבלת כאורך של וקטור דו-ממדי ששני רכיביו מתפלגים נורמלית, עם תוחלת אפס ואותה סטיית תקן. למשל, אם הסטיות של קליע מן המטרה מתפלגות נורמלית בציר X ובציר Y, ובלתי תלויות זו בזו, אז מרחק הקליע מן המטרה מתפלג לפי התפלגות ריילי.

ההתפלגות תלויה בפרמטר ${\displaystyle \ \sigma }$, המציין את סטיית התקן של הרכיבים בווקטור.

פונקציית הצפיפות היא ${\displaystyle f(x|\sigma )={\frac {x\exp \left({\frac {-x^{2}}{2\sigma ^{2}}}\right)}{\sigma ^{2}}}.}$.

המומנטים נתונים על ידי עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mu_k=\sigma^k2^{k/2}\,\Gamma(1+k/2)\,} ,

כאשר ${\displaystyle \ \Gamma }$ מסמנת את פונקציית גמא.

בפרט, מתקבלים:

התוחלת עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \sigma \sqrt{\frac{\pi}{2}}} ,

השונות ${\displaystyle {\frac {4-\pi }{2}}\sigma ^{2}}$,

הצידוד עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \frac{2\sqrt{\pi}(\pi - 3)}{(4-\pi)^{3/2}}}

והגבנוניות ${\displaystyle -{\frac {6\pi ^{2}-24\pi +16}{(4-\pi )^{2}}}}$.

אמידת פרמטרים

בהינתן מדגם בן N ערכים בלתי תלויים ושווי התפלגות מהתפלגות ריילי עם פרמטר ${\displaystyle \sigma }$ (שאינו ידוע), אומד הנראות המקסימלית של הפרמטר נתון על ידי הנוסחה עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \hat{\sigma}=\sqrt{\frac{1}{2N}\sum_{i=1}^N x_i^2}.}

התפלגויות דומות

• אם ${\displaystyle \ X,Y\sim N(0,\sigma ^{2})}$ משתנים נורמליים בלתי תלויים, אז עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ R = \sqrt{X^2 + Y^2} \sim \mathrm{Rayleigh}(\sigma)} מתפלג לפי התפלגות ריילי (מכאן הפרמטר סיגמא).
• אם ${\displaystyle \ R\sim \mathrm {Rayleigh} (1)}$, אז ${\displaystyle \ R^{2}}$ מתפלג התפלגות כי בריבוע עם שתי דרגות חופש.
• אם עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ X} מתפלג התפלגות אקספוננציאלית, עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ X \sim \mathrm{Exponential}(x|\lambda)} , אז

${\displaystyle \ Y={\sqrt {2X\sigma ^{2}\lambda }}\sim \mathrm {Rayleigh} (y|\sigma )}$.

• אם ${\displaystyle \ R\sim \mathrm {Rayleigh} (\sigma )}$ אז לסכום הריבועים עיבוד הנוסחה נכשל (MathML עם גיבוי SVG או PNG (מומלץ לדפדפנים מודרניים ולכלי נגישות): תגובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ \sum_{i=1}^N R_i^2} יש התפלגות גמא עם הפרמטרים N ו- ${\displaystyle 2\sigma ^{2}}$:

${\displaystyle \ [Y=\sum _{i=1}^{N}R_{i}^{2}]\sim \Gamma (N,2\sigma ^{2})}$.

התפלגות כי בריבוע, התפלגות רייס, התפלגות וייבול מהוות כולן הכללות של התפלגות ריילי.

התפלגות מקסוול-בולצמן היא התפלגות האורך של וקטור נורמלי תלת-ממדי, בדומה להתפלגות ריילי, המתאימה למקרה הדו-ממדי.

ראו גם

• התפלגות נורמלית
• התפלגות רייס

לקריאה נוספת

• Papoulis, A. Probability, Random Variables, and Stochastic Processes, 2nd ed. New York: McGraw-Hill, pp. 104 and 148, 1984