מטריצה משולשית
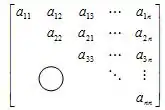

מטריצה משולשית עליונה היא מטריצה ריבועית שבה כל האיברים שמתחת לאלכסון הראשי שווים לאפס, כלומר האיברים היחידים במטריצה שאינם שווים בהכרח לאפס מופיעים במשולש העליון שמעל האלכסון הראשי (כולל האלכסון עצמו). באופן דומה, מטריצה משולשית תחתונה היא מטריצה בה כל האיברים שמעל האלכסון הראשי הם אפסים. מטריצה שהיא משולשית עליונה ומשולשית תחתונה נקראת מטריצה אלכסונית.
כל מטריצה משולשית תחתונה היא מטריצה משוחלפת של מטריצה משולשית עליונה מתאימה, ולהיפך. מהסיבה הזו ניתן להמיר כמעט כל תכונה של המטריצות המשולשיות עליונות ולתכונה מתאימה של המשולשיות תחתונות.
החישובים העוסקים במטריצות משולשיות הם נוחים יחסית. למשל, הדטרמיננטה של מטריצה משולשית היא מכפלת איברי האלכסון שלה. מכפלה של שתי מטריצות משולשיות עליונות היא מטריצה משולשית עליונה, ואיברי האלכסון שלה הם מכפלת איברי האלכסון של שתי המטריצות. תכונה זו נותנת מאפיין פשוט לנילפוטנטיות של מטריצה משולשית מעל חוג קומטטיבי - המטריצה נילפוטנטית אם ורק אם כל איברי האלכסון שלה הם איברים נילפוטנטיים. בפרט, כאשר עוסקים במטריצות מעל שדה המטריצה נילפוטנטית אם ורק אם כל איברי האלכסון הם אפסים.
ראו גם
| נושאים באלגברה לינארית | ||
|---|---|---|
| מושגי יסוד | שדה • מרחב וקטורי • משוואה לינארית • מערכת משוואות לינאריות • העתקה לינארית • מטריצה | |
| וקטורים | תלות לינארית • צירוף לינארי • קבוצה פורשת • בסיס • קואורדינטות | |
| מטריצות | כפל מטריצות • שחלוף • דטרמיננטה • דרגה • עקבה • מטריצה מצורפת • מטריצה משולשית • דמיון מטריצות • ערך עצמי • פולינום אופייני • מטריצה לכסינה • צורת ז'ורדן | |
| העתקות | העתקה לינארית • קואורדינטות • מטריצה מייצגת • גרעין (אלגברה) • אנדומורפיזם • איזומורפיזם • העתקה אפינית • העתקה פרויקטיבית | |
| מרחבי מכפלה פנימית | מכפלה סקלרית • מכפלה וקטורית • אורתוגונליות • מטריצה סימטרית • אופרטור הרמיטי • אופרטור אוניטרי • העתקה נורמלית | |
| תבניות | תבנית בילינארית • תבנית סימטרית • תבנית הרמיטית • תבנית סימפלקטית • חפיפת מטריצות • משפט סילבסטר • תבנית מולטי-לינארית אנטי-סימטרית • אוריינטציה • צפיפות • טנזור | |